2.1 Study area and data set

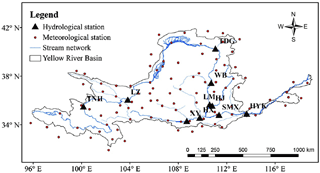
As the second longest river in China , YRB is an important agricultural production base in China, which locates in 32–42^∘ N and 94–119^∘ E. YRB has a complex surface, large heterogeneity of surface vegetation, which is sensitive to climate change and human disturbance. The annual temperature in YRB has an obviously spatial uneven, which is higher in the southeast but lower in the northwest. The precipitation mainly occurs in summer rains more, southeast rainy, northwest drought, plain precipitation is more than plateau, mountain is more than basin. The whole basin was divided into ten sub-catchments (Fig. 1), including seven catchments: Tangnaihai (TNH), Lanzhou (LZ), Toudaoguai (TDG), Hejin (HJ), Sanmenxia (SMX) and Huayuankou (HYK) with their control stations in the trunk stream, two tributary catchments Xianyang (XY) and Huaxian (HX) and an interior drainage area (located in northern YRB between Wubao (WB) and Longmen (LM) catchments).

Figure 1Distribution of 101 meteorological stations and ten hydrological stations in YRB.

Download

We collected observation data (monthly precipitation and monthly values of mean, minimum, and maximum surface air temperature) of 101 weather stations in the YRB for the period of 1961–2005, from China Meteorological Data Service Center (CMDC) (http://data.cma.cn/). The meteorological stations' data was interpolated to interpolate at a spatial resolution of 0.25^∘ × 0.25^∘ using kriging method and the temperature adjusted for differences in elevation between the two grids taking into account the lapse rate of −0.65 ^∘C for every 100 m increase in elevation. The daily streamflow data of ten hydrological stations were collected from the “China Year Books of Hydrology”.

Eight climate models for the climate change projections under the RCP4.5 and RCP8.5 scenarios (Table 1) downloaded from the Program on Climate Model Diagnosis and Intercomparison (PCMDI) website (https://esgf-node.llnl.gov/search/cmip5/). All the historical simulations are for the period of 1961 to 2005 according to the observed data time series, and the future projects of RCP45 and RCP85 cover the period of 2006–2099. Because of the difference of each climate model horizontal resolution, we used bilinear interpolation to make all the GCM climate fields at same spatial resolution (0.25^∘ × 0.25^∘) with the observations.

Table 2The RMSE of monthly precipitation and temperature between observed and downscaled model simulated in YRB from 1961–2005.

Download Print Version | Download XLSX

2.2 Equidistant quantile-based mapping method

The equidistant CDF matching (EDCDFm) statistical downscaling method developed by Li et al. (2010) was applied to bias correct the monthly precipitation and temperature fields from eight CMIP5 models in YRB. EDCDFm uses the differences between the GCMs simulate climate factors and cumulative distribution characteristics of regional observation climate to deviation correction about the climate, which is simulated by climate models. Compared the standard quantile-based mapping method (CDF), the EDCDFm can capture the extreme climate effectively, improving internal error climate model data and the limitation of the application of the method of interpolation, and then improve the accuracy of the climate simulation (Eq. 1). In this study, we applied this method first to correct the biases in the historical period (1961–2005) and then to the future period (2006–2099) for each model.

where F is the CDF of either the observations (o) or model (m) for a historic training period, current climate period (c) or future projection period (p).

2.3 Evaluation of model performance

Root mean square error (RMSE) and correlation coefficient (CC) were used to evaluate the downscaled model performance against to the observations. The RMSE and CC between a model-simulated and observation climate fields are defined as:

and,

Where M, O, ${\stackrel{\mathrm{‾}}{M}}_i$, ${\stackrel{\mathrm{‾}}{O}}_i$ are the simulated fields, observation fields, and mean of simulated fields, mean of observation fields, respectively. i is the number of spatial grid cells.

Figure 2Taylor diagram of standard deviation and correlation of observed and downscaled (a) monthly precipitation, (b) mean temperature, (c) maximum temperature, and (d) minimum temperature in YRB (1961–2005).

Download

2.4 VIC Model

VIC model is a semi distributed, physically based, macro-scale surface water and energy balance hydrological model. It can be run in either water balance mode or full water and energy balance mode. The model takes into account the land-gas water balance and energy balance, the unevenness of the spatial distribution of soil water storage capacity, considering streamflow yield under saturated storage and streamflow yield under excess infiltration, nonlinear regression of base flow. The Richards equation is used to describe the vertical one-dimensional soil water movement, and the Darcy law is used to describe the process of water vapor flux in soil layers (Zhang et al., 2009). We used observed data and eight downscaled model's outputs as the climatic forcing data of the VIC model. The VIC model has seven sensitive parameters that need to be calibrated for the study area, including the infiltration curve index (infilt), the lowest maximum base of soil flow (D_smax), base flow of nonlinear growth occurs and the proportion of the D_smax (D_s), the ratio of the bottom soil maximum moisture base flow nonlinear growth (W_s), the depth of soil layer (Depth1, Depth2, Depth3). In this study, Nash Sutcliffe coefficient (NSCE; Nash and Sutcliffe, 1970) and total relative Bias were used to evaluate the model simulations.

3.1 Assessment of downscaled outputs

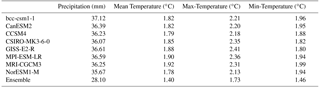
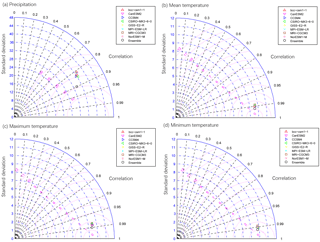
RMSE of monthly precipitation and temperature between downscaled outputs with observations were presented in Table 2. It could be found that the RMSE of eight model's ensemble for both precipitation and temperature is lower than any individual model. Among eight models, model NorESM1-M shows the smallest RMSE between precipitation, mean temperature, maximum temperature, and minimum temperature than any other model. The RMSE of monthly precipitation from individual model varies from 35.67 to 37.12 mm, and model bcc-csm1-1 has the highest RMSE value. The downscaled monthly mean temperature has lowest RMSE varies from 1.78 to 2.41^∘ than that of maximum and minimum temperature. Model MPI-ESM-LR has the highest RMSE of monthly mean temperature, model GISS-E2-R has the highest value of maximum temperature, and model MRI-CGCMS has the highest RMSE value of minimum temperature. The standard deviation and correlation using Taylor figure (Taylor, 2001) of eight models and their ensemble against to the observations (Fig. 2). The correlation coefficient of precipitation is about 0.83. Meanwhile, the monthly mean, maximum, and minimum temperature have higher correlation coefficient (around 0.99) than that of precipitation. Especially, the multi-model ensembles of precipitation and temperature present higher correlation coefficient than any single model. It shows that the multi-model ensemble can reduce the noisy of each model's simulation. Therefore, we analyzed the spatial distribution of RMSE and CC of eight model simulations against to the observations.

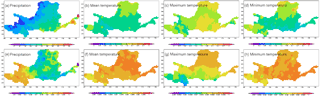
The spatial distribution of RMSE of downscaled ensemble outputs against to the observations was presented in Fig. 3. It shows that the highest RMSE occurred in the east area varies from 56 to 72 mm, while the lowest values occurred in the west area varies from 16 to 24 mm. The RMSE of the maximum and minimum temperature in the middle of north area is larger than other regions. Meanwhile, the west area has the highest correlation coefficient of precipitation varies from 0.8 to 0.9, while middle area has the lowest correlation coefficient with the observed precipitation. The mean and minimum temperature have good correlation coefficient with the observations varies from 0.98 to 0.99 for the whole basin. The correlation coefficient of the maximum temperature is lower than that of mean and maximum temperature, and the west region has the relatively lowest correlation coefficient value (about 0.96). Thus, we can conclude that these downscaled eight model's ensemble is good at simulating the precipitation and temperature in YRB.

Figure 3Spatial distribution of RMSE (a–d) and CC (e–h) showing comparison of monthly model set range simulations over the region with observations (1961–2005).

Download

3.2 VIC model calibration and validation

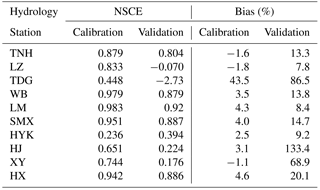
We analyzed the NSCE and Bias of the VIC model simulations with the observed streamflow of each hydrological station for calibration period and validation period (Table 3). The whole basin was divided into ten sub-catchments for calibration and validation. For nested catchments, the upstream flood wave was routed into the downstream with the Muskingum method. Then by taking the difference between observed and routed ones of downstream, the hydrograph for areas between upstream and downstream was derived and was further applied for calibration. Since no observation stations were collected for the catchments of interior drainage area and the lower reaches of HYK, parameters from their each adjacent catchment, WB and HYK respectively, were employed for computation instead. The NSCE of seven stations are above 0.7 and the bias of streamflow is around ±5 % during the calibration period (1961–1990). Meanwhile, there are five stations has a higher Nash value above 0.7 during the validation period (1991–2012). These results indicate that VIC model is good at simulating the hydrological procession of the Yellow River.

Table 3The statistics of calibration and validation periods monthly flows for the ten sub-catchments in YRB.

Download Print Version | Download XLSX

3.3 Projected changes of precipitation and temperature

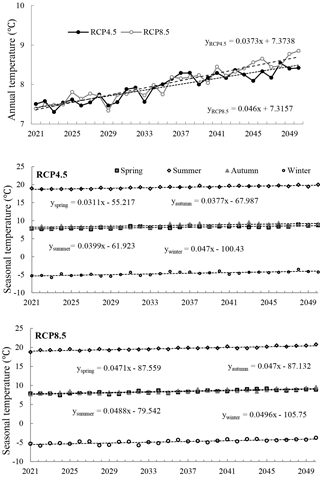
During future period of 2021–2050, the annual precipitation for two RCPs show an increase trends, and the increasing rate varies from 7.795 mm/10 a to 11.56 mm/10 a for RCP4.5 and RCP8.5, respectively (Fig. 4). Seasonal precipitation presents a slightly increasing trend in spring and autumn, while a very slightly decreasing trend with the rate of 2.99 mm/10 a in summer for RCP4.5. On the other hand, the changing trends of winter precipitation for RCP8.5 is similar with that of RCP4.5 with a higher increasing rate. Notably, the summer precipitation of RCP8.5 shows an increase trend with the rate of 2.27 mm/10 a, which is opposite to that of RCP4.5.

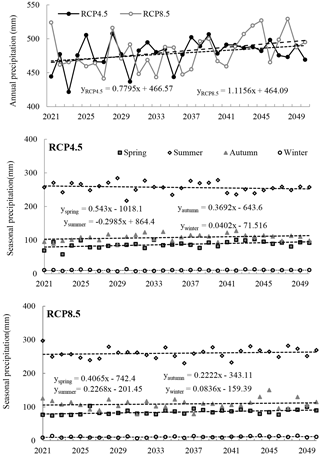
Figure 4The time series of annual and seasonal precipitation for RCP4.5 and RCP8.5 from 2021 to 2050 in YRB.

Download

During the period of 2021–2050, the basin average temperature shows an obviously increasing for two RCPs (Fig. 5). Annual mean temperature projected an increasing rate of 0.373^∘/10 a and 0.46^∘/10 a for RCP4.5 and RCP8.5, respectively. Both RCP4.5 and RCP8.5 all project an increasing trend of seasonal temperature in YRB. The changing rate of seasonal temperature for RCP8.5 more than 0.47^∘/10 a, which is higher than that of RCP4. 5. Meanwhile, the fastest increasing of seasonal temperature occur in winter with the rate of 0.47^∘/10 a and 0.50^∘/10 a for RCP4.5 and RCP8.5, respectively. The changing rate of seasonal temperature for RCP4.5 is uneven for all seasons, in which autumn is increasing more quickly (about 0.07^∘/10 a) than that of spring. Whereas RCP8.5 projects a similar increasing rate in spring and autumn, while a little higher in summer and winter.

Figure 5The time series of annual and seasonal temperature for RCP4.5 and RCP8.5 from 2021 to 2050 in YRB.

Download

3.4 Ensemble streamflow prediction

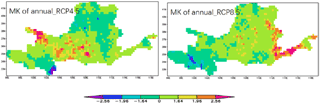
During the period of 2021–2050, the spatial distribution of MK for annual streamflow for RCP4.5 scenario shows an obviously increasing trend in the middle of the basin, while decreasing in the west and north parts of basin. RCP8.5 projects a different trend of annual runoff with RCP4.5, which remarkable increasing in the east part of basin and decreasing in the west part of basin (Fig. 6). Seasonal streamflow of basin average for RCP4.5 and RCP8.5 show a slightly increasing trend except in summer of RCP4.5, which shows a slightly decreasing trend.

Figure 6MK trend of annual streamflow for RCP4.5 and RCP8.5 from 2021 to 2050 in YRB.

Download

Notably, the spatial distribution of MK test for seasonal streamflow shows an uneven spatial changing trend (Fig. 7). For example, the streamflow shows a remarkable increasing trend in the sub-catchment of LZ in spring and autumn, while which shows a slightly decreasing trend in summer for RCP4.5. For the middle parts of YRB, the streamflow presents an unobvious decreasing trend in summer, while increasing in spring. For RCP8.5, streamflow of north parts of YRB shows a slightly increasing trend except the upstream region. Notably, the streamflow in upstream of YRB shows an obviously decreasing trend in summer and autumn for RCP8.5, while which shows an increasing trend in spring.

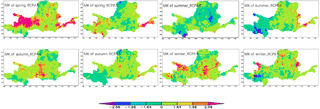
Figure 7The spatial distribution of Mann-Kendall trend test of the streamflow during 2021 to 2050 in the YRB for two scenarios.

Download

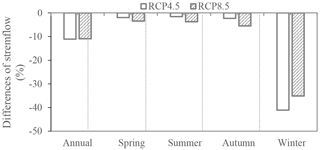
Figure 8Projected changes of annual and seasonal streamflow (2021–2050) against to the base line period (1961–1990) for RCP4.5 and RCP8.5 in YRB.

Download

For further analysis of the changing trend of streamflow in YRB for the future period, we compared the changes of future streamflow with that of base period (1961–1990) in Fig. 8. In the future period, the VIC model simulated annual and seasonal streamflow reduce obviously compared with the base period. The annual streamflow will reduce about 10 % for two RCPs. The seasonal streamflow projected a reduce ratio of 3.44, 3.70, and 5.48 % in spring, summer, and autumn for RCP8.5, respectively, which is bigger than that of RCP4.5. Especially, the streamflow projected a remarkable reduce in winter about 41.11 and 35.11 % for RCP4.5 and RCP8.5, respectively.