the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
An assessment of temporal effect on extreme rainfall estimates
Samiran Das
Dehua Zhu
Cheng Chi-Han
This study assesses the temporal behaviour in terms of inter-decadal variability of extreme daily rainfall of stated return period relevant for hydrologic risk analysis using a novel regional parametric approach. The assessment is carried out based on annual maximum daily rainfall series of 180 meteorological stations of Yangtze River Basin over a 50-year period (1961–2010). The outcomes of the analysis reveal that while there were effects present indicating higher quantile values when estimated from data of the 1990s, it is found not to be noteworthy to exclude the data of any decade from the extreme rainfall estimation process for hydrologic risk analysis.
The temporal assessment of rainfall extremes is necessary to understand its temporal behavior which will lead to better assess the frequency of extreme rainfall under climate change, and subsequently the flood risk. Since the climate change (e.g. IPCC, 1995) phenomena emerges, a large number of studies appear to find its impact on rainfall. Among them, a substantial research was carried out on rainfall extremes (Bülow et al., 2015; Das et al., 2013; Feng et al., 2007; Ntegeka and Willems, 2008; Su et al., 2008; Tabari et al., 2014; Zhang et al., 2008) as they impact the society most. The outcome is not one dimensional- a significant variability is observed in some regions whereas in some cases, a number of regions do not show much variation that prove to be significant (e.g. Alexander et al., 2006; Damberg and AghaKouchak, 2014; Feng et al., 2007). The data length and type of diagnostic tools can also influence the outcome (Ntegeka and Willems, 2008). A regional behavior is also recognized in those studies (Alexander et al., 2006).
The Mann Kendall and the Spearman rho tests are mostly used approaches to assess the temporal variability. In a more recent time, the quantile perturbation method (Ntegeka and Willems, 2008; Tabari et al., 2014) is used to assess the decadal variability in terms of identify the changes in the extremes for particular return periods. The peak-over-threshold (POT) data was used so that a longer data series can be gathered in a decade. All the above approaches are non-parametric.
This study introduces a new parametric approach to assess the temporal variability of rainfall extremes for the Yangtze River Basin, a major development area of China. A number of studies were carried out to investigate observed long-term trends and patterns in extreme precipitation events in china (e.g. Fu et al., 2013) including the Yangtze Basin (e.g. Su et al., 2008) in order to assess the regional response to climate change. A summary of the outcomes was reported, among others, by Chen et al. (2012) who also recognized that only a few studies were concentrated on to assess decadal variability of rainfall extremes. This study aims to investigate the issue further in terms of inter-decadal variability of extreme daily rainfall of stated return period relevant for hydrologic risk analysis. In particular, the study aims to address the following research objectives:
-
whether climate change has a significant role in decadal quantile variability of daily rainfall extremes in Yangtze Basin context
-
whether recent datasets really provide more reliable predictions of design extreme rainfall to be used in engineering purposes
The approach examines whether rainfall quantiles estimated for a decade as well as the most recent changes in extreme quantiles can be qualified as statistically significant in comparison with the natural temporal variability. A major drawback of performing decadal variability in a parametric setup is that a limited number of data set is available in a decade to fit with the selected probability model. In this study, a regional approach in region-of-influence (ROI) form (Burn, 1990; Das and Cunnane, 2012; Institute of Hydrology, 1999) is used to study the decadal quantile behavior. The ROI method is an objective way of forming a homogeneous pooling group/region for a site with limited data aiming to perform a frequency analysis. In this approach, annual maximum rainfall series are pooled from other homogeneous stations and perform frequency analysis based on index-flood method (Dalrymple, 1960). The estimation of PT, T-year return period rainfall depth, based on this approach involves derivation of a growth curve XT which shows the relation between XT and the return period T where and PI is the index measurement (e.g. mean or median of the at-site annual maximum rainfall series) at the site of interest (Das, 2017). A suitable probability distribution function is required to estimate quantiles. A detailed explanation of the method including the criteria that form homogeneous groups can be obtained from Das (2017). This study uses geographical proximity to group stations which give promising results in many ROI based extreme rainfall study (Kyselý et al., 2011; Reed et al., 1999). The 5T rule (Institute of Hydrology, 1999) (the total number of station years of data to be included when estimating the T year event) is applied to delineate the size of the group for a subject location. Finally the homogeneity is assessed by the Hosking-Wallis heterogeneity measure H1 (Hosking and Wallis, 1997). The ROI regional approach is appealing because it reduces the variability of the estimates and reflects the changes in a best possible manner.
With this approach, a homogeneous pooling/regional group for a particular decade is selected from gauged stations that are available in that particular decade and a frequency analysis is performed for a target site. A decade consists of 10 annual maximum (AM) data points but with this approach a large number of AM data is available for that particular decade which will lead to achieve a reliable estimate.
In order to test whether the variability is statistically significant, the study outlines confidence intervals based on a parametric Monte Carlo method. In this test, a baseline AM rainfall series is first fitted to a distribution after which random samples are generated from the distribution, and confidence intervals are estimated. In the present study, the baseline series is chosen as the long-term historical datasets from which the base quantile is estimated while the other one is from the group of series taken from a particular decade of interest. After assessing the decadal variability, the confidence intervals are also estimated and overlaid on the same chart. It is therefore graphically possible to identify periods that demonstrate significant departures under the hypothesis of no trend of rainfall extremes.
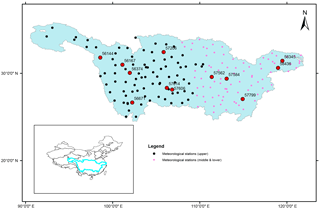
This study selects Yangtze River Basin to analyze decadal behavior in annual maximum (AM) daily rainfall series of over a 50-year period (1961–2010). The basin is analyzed with two major distinct climatic conditions: upper and middle-lower. A total number of 180 stations are available in the study area. They are displayed on the map in Fig. 1. The datasets were obtained from the National Meteorological Information Center of China Meteorological Administration (CMA). Data of these stations have different record length and have different starting and ending year.
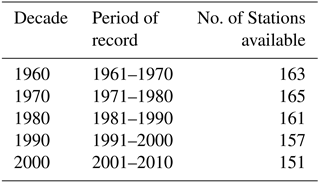
Table 1 lists the number of stations that are available for each decade. Only stations which have a minimum of 9 years of data available are included for that particular decade. There are 144 stations for which AM data are available for 5 decades.
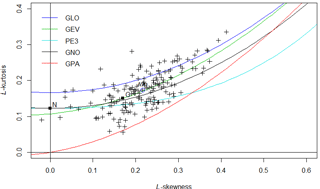
In a parametric approach, a suitable probability distribution is needed to describe the data. The L-moment ratio diagram (Das, 2016; Hosking and Wallis, 1997) is used to identify an appropriate distribution. The LMRD diagram shown in Fig. 2 identifies the generalized extreme value (GEV) as the most suitable distribution for the Yangtze Basin. The formula for estimating growth factors and the associated quantiles based on the GEV can be obtained from Das and Cunnane (2011).
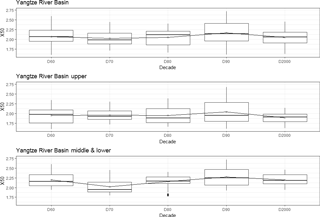
Growth factors, XT (e.g. standardized values) estimated for each decade of 144 stations are analyzed first to show the general temporal behavior. The study analyzes extremes in terms of 50 year return period values (X50). They are estimated based on pooling groups of size 250 station-year (i.e. 25 stations) that satisfy the 5T rule. For each of these 144 stations, the pooling group for particular decade was selected from stations that are available in that particular group. The values of X50 for each decade for each station are displayed in Box-Plot form in Fig. 3. The largest average X50 value occurs in decade 90 for both the Upper and the Middle-Lower reaches. The average smallest value occurs in decade 70. The upward trend of average X50 in decade 90 is the main contribution to the increase in extreme rainfall in the Yangtze Basin, which can partly explain the intensification of flooding in the 1990s which was also noticed by Su et al. (2008). But the trend decreased in the following decade indicating that it is not worthwhile to take only recent data for frequency analysis.
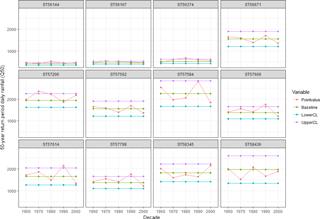
This method also permits to identify whether the decadal variability occurred in an individual station is significant or not. A number of stations shown bold in Fig. 1 are chosen to represent for that particular region. They can be classified as Upper (Upper-West stations 56144, 56167, 56374; Upper-South station 56671; Upper-North station 57206; Upper-East stations 57614, 57606), Middle (stations 57562, 57584, 57799) and Lower (stations 58345, 58436). The decadal quantile, P50 of rainfall extremes are shown in Fig. 4. The confidence intervals in Fig. 4 represent the 95 % bounds of random variation under the null hypothesis of no trends.
The different decade's values (anomalies) came out significant for different location of Yangtze basin. In the Upper-West basin, the 1980 decade value of P50 is larger than those of the other decades with some cases significant values were also observed for that decade. However, the quantiles are significantly lower than those of the other parts of the Yangtze Basin. The 1970 decade value of P50 came out significant for station 57206. The decadal values of 1990s provide largest values for the Upper-East and Middle region. In many cases they are found to be significant which is in line what is observed by Su et al. (2008) that partly explain the frequent occurrence of floods in the 1990s. The decadal quantile values for the decade 2000 came out as the largest for Lower region but they are not proved to be significant which is similar what is found by Zhang et al. (2008).
This study examines the decadal variability in daily AM rainfall series of Yangtze River Basin over a 50-year period (1961–2010) with a novel regional parametric approach. Based on the dimensionless standardized growth factor of 50 year return period value, the average largest value occurred in the 1990s but a dip occurred in the following decade. There are some case studies conducted to see the nature of the decadal variability in several stations of the Yangtze Basin with significant test. In general, the 1980s decadal quantile value came out as the largest in the far Upper, the 1990s value came out as the largest in the Middle with some being proved significant, and the 2000s value came out as the largest for the lower basin. So far the outcome of the analysis reveal that while there were small effects present indicating higher quantile values when estimated from data of decade 1990, it is found not to be worthwhile to exclude the data of any decade from the extreme rainfall estimation process for hydrologic risk analysis.
The observed daily rainfall data series of selected stations were obtained from the National Meteorological Information Center of China Meteorological Administration (CMA). CMA owns the datasets and a formal request is required to obtain the required datasets.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Innovative water resources management – understanding and balancing interactions between humankind and nature”. It is a result of the 8th International Water Resources Management Conference of ICWRS, Beijing, China, 13–15 June 2018.
The research is funded by Nanjing University of Information Science and
Technology in the form of a grant (Grant no. 2243141501015) of the first
author.
Edited by: Dingzhi Peng
Reviewed by: Qinglan Li and one anonymous referee
Alexander, L. V., Zhang, X., Peterson, T. C., Caesar, J., Gleason, B., Klein Tank, A. M. G., Haylock, M., Collins, D., Trewin, B., Rahimzadeh, F., Tagipour, A., Rupa Kumar, K., Revadekar, J., Griffiths, G., Vincent, L., Stephenson, D. B., Burn, J., Aguilar, E., Brunet, M., Taylor, M., New, M., Zhai, P., Rusticucci, M., and Vazquez-Aguirre, J. L.: Global observed changes in daily climate extremes of temperature and precipitation, J. Geophys. Res.-Atmos., 111, 1–22, https://doi.org/10.1029/2005JD006290, 2006.
Bülow, I., Henrik, G., and Dan, M.: Long term variations of extreme rainfall in Denmark and southern Sweden, Clim. Dynam., 44, 3155–3169, https://doi.org/10.1007/s00382-014-2276-4, 2015.
Burn, D. H.: Evaluation of regional flood frequency analysis with a region of influence approach, Water Resour. Res., 26, 2257–2265, 1990.
Chen, H., Sun, J., and Fan, K.: Decadal features of heavy rainfall events in eastern China, Acta Meteorol. Sin., 26, 289–303, https://doi.org/10.1007/s13351-012-0303-0, 2012.
Dalrymple, T.: Flood frequency methods, U.S. Geol. Surv. 1543-A, 11–51, 1960.
Damberg, L. and AghaKouchak, A.: Global trends and patterns of drought from space, Theor. Appl. Climatol., 117, 441–448, https://doi.org/10.1007/s00704-013-1019-5, 2014.
Das, S.: An assessment of using subsampling method in selection of a flood frequency distribution, Stoch. Env. Res. Risk A., 31, 1–13, https://doi.org/10.1007/s00477-016-1318-3, 2016.
Das, S.: Performance of region-of-influence approach of frequency analysis of extreme rainfall in monsoon climate conditions, Int. J. Climatol., 37, 612–623, https://doi.org/10.1002/joc.5025, 2017.
Das, S. and Cunnane, C.: Examination of homogeneity of selected Irish pooling groups, Hydrol. Earth Syst. Sci., 15, 819–830, https://doi.org/10.5194/hess-15-819-2011, 2011.
Das, S. and Cunnane, C.: Performance of flood frequency pooling analysis in a low CV context, Hydrolog. Sci. J., 57, 433–444, https://doi.org/10.1080/02626667.2012.666635, 2012.
Das, S., Millington, N., and Simonovic, S. P.: Distribution choice for the assessment of design rainfall for the city of London (Ontario, Canada) under climate change, Can. J. Civil. Eng., 40, 121–129, https://doi.org/10.1139/cjce-2011-0548, 2013.
Feng, S., Nadarajah, S., and Hu, Q.: Modeling Annual Extreme Precipitation in China Using the Generalized Extreme Value Distribution, J. Meteorol. Soc. Jpn., 85, 599–613, https://doi.org/10.2151/jmsj.85.599, 2007.
Fu, G., Yu, J., Yu, X., Ouyang, R., Zhang, Y., Wang, P., Liu, W., and Min, L.: Temporal variation of extreme rainfall events in China, 1961–2009, J. Hydrol., 487, 48–59, https://doi.org/10.1016/j.jhydrol.2013.02.021, 2013.
Hosking, J. R. M. and Wallis, J. R.: Regional frequency analysis: an approach based on L-moments, Cambridge University Press, 1997.
Institute of Hydrology: Flood Estimation Handbook, Vol. 1–5, Institute of Hydrology, Wallingford, UK, 1999.
IPCC: Climate Changes 1995, Contribution of Working Group I to the Second Report of the Intergovernmental Panel on Climate Change, 141–193, 1995.
Kyselý, J., Gaál, L., and Picek, J.: Comparison of regional and at-site approaches to modelling probabilities of heavy precipitation, Int. J. Climatol., 31, 1457–1472, https://doi.org/10.1002/joc.2182, 2011.
Ntegeka, V. and Willems, P.: Trends and multidecadal oscillations in rainfall extremes, based on a more than 100-year time series of 10 min rainfall intensities at Uccle, Belgium, Water Resour. Res., 44, https://doi.org/10.1029/2007WR006471, 2008.
Reed, D. W., Faulkner, D. S., and Stewart, E. J.: The FORGEX method of rainfall growth estimation II: Description, Hydrol. Earth Syst. Sci., 3, 197–203, https://doi.org/10.5194/hess-3-197-1999, 1999.
Su, B., Gemmer, M., and Jiang, T.: Spatial and temporal variation of extreme precipitation over the Yangtze River Basin, Quaternary Int., 186, 22–31, https://doi.org/10.1016/j.quaint.2007.09.001, 2008.
Tabari, H., AghaKouchak, A., and Willems, P.: A perturbation approach for assessing trends in precipitation extremes across Iran, J. Hydrol., 519, 1420–1427, https://doi.org/10.1016/j.jhydrol.2014.09.019, 2014.
Zhang, Q., Xu, C. Y., Zhang, Z., Chen, Y. D., Liu, C. L., and Lin, H.: Spatial and temporal variability of precipitation maxima during 1960–2005 in the Yangtze River basin and possible association with large-scale circulation, J. Hydrol., 353, 215–227, https://doi.org/10.1016/j.jhydrol.2007.11.023, 2008.