the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Horizontal insulating barriers as a way to protect groundwater
Renata Cicha-Szot
Krzysztof Labus
Sławomir Falkowicz
Norbert Madetko
Trenchless Technology of Forming Horizontal Insulating Barriers (TFHB) can be considered a method of groundwater protection against inflow of pollutants. In TFHB technology, the working fluid (sodium silicate solution) and the gelling agent (CO2) are injected separately, using one tool, to different zones of the aquifer profile. Carbon dioxide injected into the saturation zone rises due to buoyancy forces and reaches the silicate which was injected at the water table level. This initiates the process of silicate gelation, resulting in the formation of an insulating barrier. For technological purposes, the gelation time must be controlled, and the resulting gel must have certain mechanical properties. In order to apply THFB in real conditions it was necessary to identify important technological and technical parameters, as well as to define interactions between the injected fluid and the aquifer rocks. Geochemical modelling (equilibrium, reaction path and reactive transport) was used to identify potential geochemical effects of the application of TFHB in sandy aquifers. Certain petrophysical parameters and mineralogical assemblages of aquifers were addressed, taking into account both low and strongly mineralized groundwater. The simulations revealed that TFHB does not have a negative impact on the chemistry of rock-water systems described in this work.
Protection of groundwater resources is a key challenge in the 21st century. New technologies are crucial in order to prevent pollution not only close to urban settings with highly congested infrastructure, but also in the case of demanding topographical relief. Trenchless Technology of Forming Horizontal Insulating Barriers (TFHB) can be considered an emergency form of immediate groundwater protection against inflow of pollutants, e.g. from hazardous landfill; however, so far there is no approved insulating technology which does not require the displacement of waste.
Trenchless methods seem to be effective; however, for the optimum solution a combination of numerous factors should be considered, including materials and geotechnical aspects. One advantage of the developed TFHB technology in shallow groundwater aquifers is the injection of a non-toxic, environmentally friendly modified water solution of sodium silicate. The set of additives which enable hybrid gelation mechanisms are determined by the composition and properties of the applied sodium silicate gels and the complex chemical reactions which cause reduced hydraulic conductivity.
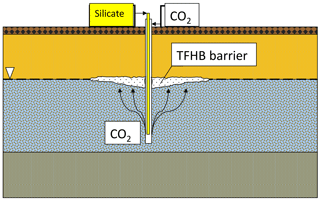
The idea of injecting sodium silicate with CO2 into geological formations has existed since 1946 (Anderson, 1946). In TFHB technology, the working fluid (sodium silicate solution) and the gelling agent (carbon dioxide) are injected separately, using one tool, to different zones of the aquifer profile. Carbon dioxide, injected into the saturation zone, rises due to buoyancy and reaches the silicate injected at the water table level.
This initiates the process of silicate gelation, resulting in the formation of an insulating barrier of expected shape and size, as shown in Fig. 1. It is assumed that a barrier formed in this way will eliminate or significantly reduce vertical filtration of liquids, eliminating the paths by which pollutants migrate into aquifers. For technological purposes, the gelation time must be controlled, and the resulting gel must have certain mechanical properties.
An important element of TFHB technology is the treatment fluid, which is based on sodium silicate water solution and characterized by low viscosity. The use of special additives allows the resistance of the gel to chemical, thermal and pressure factors to be increased. Nano-additives cause the injected liquid to turn into a gel after about 48 h, even in limited contact with CO2. Initial injection of CO2 is, however, necessary to prevent the injected silicate migrating downwards in the aquifer. The resistance of the resulting gel against hydraulic breakthrough is high, and it can reach 56.6 MPa in sandstones (Nasr-El-Din and Taylor, 2005).
CO2 injection is an important step in TFHB technology. The gas plume of carbon dioxide injected to an aquifer with a drilling tool should ideally have the shape of a paraboloid or inverted cone, with a height equal to the depth of the gas injection in the aquifer. A similar phenomenon is used in the removal of hydrocarbon-based pollutants from soil and shallow aquifers by the method of aeration (air sparging). Air sparging is technology in which air is injected below the water table through a drilling tool fitted with a special screen. The injected air migrates upwards, initiating an aerobic decontamination processes in polluted aquifers. Air sparging was implemented in the mid-1980s in Germany to enhance the process of removing chlorinated solvents from shallow aquifers. It was also used in the United States to clean up saturated zones contaminated with gasoline and other volatile contaminants (Johnson et al., 1993).
In most cases the horizontal permeability (kh) of porous aquifer formations is higher (up to 30 times) than the vertical permeability (kv). This has a beneficial effect on TFHB barrier formation because the greater the kh∕kv ratio, the easier and the more efficient the lateral injection of silicate solution into an aquifer. Moreover, the greater the permeability anisotropy, the more the shape of the injected gas cloud forms a paraboloid.
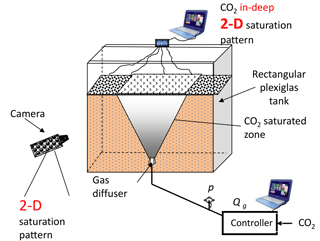
Laboratory flow visualization experiments using glass beads and sand as a porous medium were carried out to study CO2 sparging. The aim of the experiments was to determine the effect of the gas injection method and heterogeneity of the porous media on the gas flow pattern. In order to visualize the experimental results, we built the laboratory setup shown in Fig. 2. It consists of a relatively thin rectangular tank ( cm) made of Plexiglas and filled with porous medium and tap water.
The CO2 gas is supplied through a cylindrical diffuser placed at bottom centre of the tank. The gas rate is operated by a flow controller in a continuous and cyclic manner.
Digital photos were taken to evaluate the geometry of the gas plume. Additionally, continuous scanning of conductivity confirmed the changes inside the porous medium. Different sands and spherical glass beads were used separately to test the effect of grain size and shape on the gas flow structure. The example results are shown in Fig. 3. Three distinct gas flow patterns were observed, depending both on grain shape and gas injection method. In the case of spherical glass beads, the channel type flow pattern shown in Fig. 3a was observed; however, for the non-spherical sands the geometry of gas flow depends primarily on the continuous or cyclic regime of the gas injection. When gas was injected in cyclic way (Fig. 3c) the gas plume was wider compared to the continuous regime (Fig. 3b).
Non-toxicity and environmental friendliness are the basic conditions for the application of TFHB technology in shallow aquifers. Moreover, it is also important that the injected working fluid (silicate solution) and the CO2 gas (gelling catalyst) do not cause adverse or unpredictable interactions with the aquifer, including rapid and radical changes in pH; however, the dissolution of primary minerals combined with the crystallization of secondary phases can have a beneficial effect on the reduction of porosity. Therefore, the potential geochemical effects of the application of TFHB in the example aquifers were identified with the aid of simple geochemical simulations (Labus et al., 2015; Suchodolska and Labus, 2016).
Three types of dynamic modelling (equilibrium, reaction path and reactive transport) were performed on static geological aquifer models with similar petrophysical parameters but different mineralogical composition, taking into account both fresh and highly mineralized waters. The simulations performed do not relate to the effects of the pore space being blocked by silicate gels. They allow the analysis and forecasting of geochemical phenomena occurring in the aquifer systems due to the injected silicate solution.
Interactions between the injected solutions and the aquifer rock matrix and pore water were simulated by means of the Geochemists' Workbench Package (GWB, Bethke, 2008) for the following systems, each with 20 % porosity:
-
aquifer composed of quartz sand (80.0 %) with 0.01 % Fe (OH)3
-
quartz sand (79.9 %) and calcite (0.1 %),
-
quartz sand (79.9 %) and calcite (0.1 %) with 0.01 % Fe (OH)3,
-
quartz sand (77 %) and clay minerals (3 % illite)
-
quartz sand (80.0 %) with seawater,
-
quartz sand (80.0 %) with seawater, using pre-treatment pad fluid injection,
-
quartz sand (79.9 %) and dolomite (0.01 %).
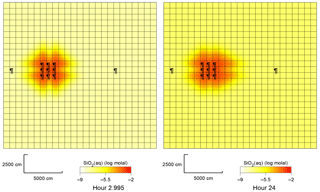
Figure 4Plan view of SiO2(aq) concentrations around the group of 9 injection wells, in quartz aquifer, 3 and 24 h after the silicate fluid injection.
4.1 Two-dimensional model of transport and reaction
The aim of the two-dimensional transport and reaction models was to follow the development of changes in the simulated aquifer, taking into account changes in the hydrodynamic field. GWB's X2t package was applied in this simulation. The model domain simulates a 200 m × 200 m section of an aquifer that is 0.5 m thick and is composed of 625 nodal blocks, each of which is 8 m × 8 m. The following parameters were considered: porosity, 20 %; permeability, 1-D; transverse dispersivity, 0.2; longitudinal dispersivity, 1 m; diffusion coefficient, cm2 s−1. Groundwater flow across the domain is controlled by a hydraulic gradient of 0.05 between the left boundary (inflow) of the model and the right boundary (outflow). Injection wells (9 wells situated in a square grid) are located in the left part of the model; the silicate solution is injected within 3 h with the rate of 1.5 m3 h−1 in each well. It was assumed that the injection of the working liquid into the aquifer environment would cause changes in the pore water chemistry as well as in the mineralogical composition of the aquifer matrix.
For a solute the rate of accumulation of a component in the groundwater is the sum of the rate due to transport, and thechemical reactions, Eq. (1):
where: φ is porosity, Ri is reaction rate (mol cm−3 s−1), Ci is the component's concentration, Dxx is the entries in the dispersion tensor, and (υx, υy) is groundwater velocity vector (Bethke, 2008).
It was found that in all cases the injection of silicate solution triggers the pH rise within a range of about 10 m from the axis of the injection well. In the quartz sand aquifer, the quartz mineral slowly dissolves and the concentration of dissolved SiO2 increases, as shown in Fig. 4.
In the modelled systems that included 0.1 % vol. of carbonate rocks and 0.01 % vol. of Fe(OH)3, the dissolution of small volumes of calcite was also found; this precipitated back after the injection was terminated.
In the systems with illite, the effects of its hydrolysis were observed: precipitation of secondary kaolinite, release of potassium cations, and intensification of the decrease in pH.
During simulation of injection of silicate solution into the aquifer with seawater, it was noted that the pH change is limited practically to the well skin zone. Considering the actual, wider migration range of the injected liquid, this phenomenon may have consequences for the gelation time of the silicate. In order to extend the gelation time, the alkalinity of the injected solution should be increased, and/or the pad fluid should be used prior to the silicate solution injection. The injection zone located in the aquifer in equilibrium with seawater is prone to secondary dolomite precipitation, the volume of which is however small and reaches 0.0013 % vol.
4.2 Kinetic reaction path modelling
The performed reaction path simulation (simulation of reaction sequences) made it possible to determine the impact of chemical processes on the geochemical composition of porous media filled with a silicate solution. CO2 was injected to accelerate sol-gel transition of the silicate solution. This led to geochemical composition changes which increased CO2 partial pressure. The GWB React package was applied in this modelling. The following kinetic dissolution/precipitation rate equation was used in the calculations Eq. (2):
where rk is reaction rate (mol s−1), dissolution is rk>0, precipitation is rk<0), As is the mineral's surface area (cm2), kT is the rate constant (mol cm−2 s−1) at temperature T, Q is the activity product (–), K is the equilibrium constant for the reaction (–). According to the above equation a given mineral precipitates when it is supersaturated or dissolves when it is undersaturated at a rate proportional to its rate constant and the surface area.
In all modelled aquifers, CO2 injection causes a decrease in pH to about 5.8.
Small amounts of iron are released in the aquifer composed of quartz sand with iron (III) hydroxide due to the decomposition of Fe(OH)3, as shown in Fig. 5. The solution of the treatment fluid in pore waters is oversaturated for SiO2 phases and Ca(FeO2)2, and undersaturated for carbonates and sulphates. The crystallization of mineral phases of SiO2 has a negligible effect on porosity.
In the presence of Fe(OH)3 in the aquifer containing small amounts of calcite, a slight increase in porosity is observed, mainly related to the decomposition of CaCO3. This process is responsible for the increase of Ca2+ concentrations and for the decrease of sulphate concentration, due to the synthesis and subsequent sorption of CaSO4. Precipitation of silica and a release of small amounts of iron is also noticeable.
Decomposition of illite, amorphous silica and Fe(OH)3, and the subsequent crystallization of secondary nontronite-Na has virtually no effect on the porosity in the sandy aquifer with illite.
In the aquifers saturated with seawater, the pH of the solution drops more to about 5.2 after injection of CO2. Precipitation of quartz and decomposition of dolomite practically does not affect the porosity of the system. After the injection of CO2, a high undersaturation with carbonate phases is observed, whereas the tendency of amorphous silica to precipitate increases.
4.3 One-dimensional transport and reaction model
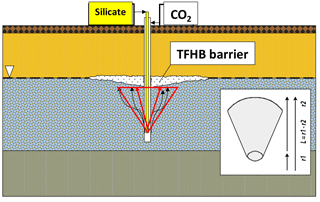
The one-dimensional transport and reaction model was introduced to simulate the interactions and geochemical changes along the flow path of CO2 injected below the injected silicate solution into the zone of saturation to accelerate the gelation process, as shown in Fig. 6; GWB's X1t package was applied. The flow field is simulated in the spherical domain with an internal radius of r1=5 cm and an external radius of r2=205 cm; this corresponds to the gas migration path, L=200 cm. The domain consists of 10 cells of equal heights.
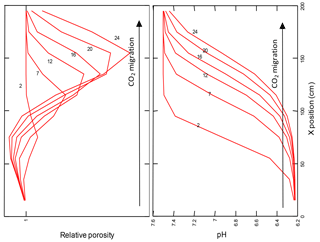
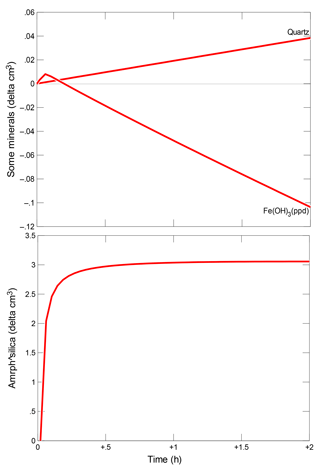
Figure 7Relative porosity, and pH changes along the flow path of CO2 injected into the zone of saturation.
During the injection of CO2, the pH of pore waters in the modelled aquifer decreases. The strongest and fastest changes in pH are visible in the initial cells of the model, as shown in Fig. 7.
The increase in CO2 fugacity and ion concentrations in pore water is most pronounced in the initial cells of the model in the proximity of the injection point. As a result of the decomposition of the dolomite in the initial cell and its crystallization in subsequent cells of the model, an increase or decrease in porosity is observed, respectively. The porosity extremes change over time, according to the direction of CO2 transport in pore waters, see Fig. 7. The mineralogical changes of the rock matrix and the chemical composition of the pore fluid observed in all models are very small.
Under real conditions, not a single-phase solution in equilibrium with CO2, but a two-phase CO2+H2O fluid will be transported through the aquifer. In this case, the migration rate will increase as the fluid moves upwards into the lower pressure zones, where the gas bubbles expand, the density of the CO2+H2O two-phase fluid decreases, and its transport is accelerated.
The experiments indicated that the gas flow regime in a saturated porous medium varies greatly as result of heterogeneity and anisotropy of the porous medium.
Geochemical modelling (equilibrium, reaction path and reactive transport) was used to identify potential geochemical effects of the application of TFHB in sandy aquifers. Certain petrophysical parameters and mineralogical assemblages of aquifers were addressed, taking into account both low and highly mineralized groundwater. The simulations revealed that the TFHB does not have a negative impact on the chemistry of the rock-water systems considered.
The data that support the findings of this study are available on request from the corresponsing author Krzysztof Labus (krzysztof.labus@polsl.pl). The data are not publicly available due to co financing of the research project by private company.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Innovative water resources management – understanding and balancing interactions between humankind and nature”. It is a result of the 8th International Water Resources Management Conference of ICWRS, Beijing, China, 13–15 June 2018.
This work is the result of research conducted within the research project “A
novel environmentally friendly technique of creating horizontal barriers in
water-bearing zones”, funded by the National Centre for Research and
Development within the Smart Growth Operational Programme Priority axis 1:
SUPPORT FOR R&D ACTIVITY OF ENTERPRISES Priority 1.1.1: R&D projects of
enterprises, Contract No.: POIR.01.01.01-00-1038/15-00.
Edited by: Bo Pang
Reviewed by: Meifang Ren
and one anonymous referee
Anderson, K. H.: Method of Oil Recovery, U.S. Patent 2,402,588, 1946.
Bethke C. M.: Geochemical and biogeochemical reaction modelling, Cambridge Univ. Press, Cambridge, 1–543, 2008.
Johnson, R. L., Johnson, P. C., McWhorter, D. B., Hinchee, R. E., and Goodman, I.: An overview of in situ air sparging, Ground Water Monit. Remediat., 13, 127–135, https://doi.org/10.1111/j.1745-6592.1993.tb00456.x, 1993.
Labus, K., Tarkowski, R., and Wdowin, M.: Modeling gas–rock–water interactions in carbon dioxide storage capacity assessment: a case study of Jurassic sandstones in Poland, Int. J. Environ. Sci. Technol., 12, 2493–2502, https://doi.org/10.1007/s13762-014-0652-6, 2015.
Nasr-El-Din, H. A. and Taylor, H. C.: Evaluation of sodium silicate/urea gels used for water shut-off treatments, J. Pet. Sci. Eng., 48, 141–160, 2005.
Suchodolska, K. and Labus, K.: Simplified models of transport and reactions in conditions of CO2 storage in saline aquifers, Energy Proced., 97, 509–514, https://doi.org/10.1016/j.egypro.2016.10.062, 2016.