Mid and long-term optimize scheduling of cascade hydro-power stations based on modified GA-POA method

Li, Jiqing; Yang, Xiong

doi:https://doi.org/10.5194/piahs-379-199-2018

Articles | Volume 379

https://doi.org/10.5194/piahs-379-199-2018

Articles | Volume 379

Pre-conference publication

05 Jun 2018

Pre-conference publication |

| 05 Jun 2018

Mid and long-term optimize scheduling of cascade hydro-power stations based on modified GA-POA method

Jiqing Li and Xiong Yang

Abstract

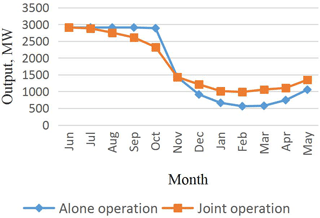
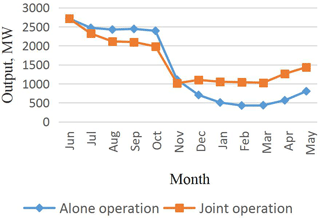
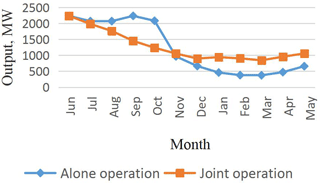
In this paper, to explore the efficiency and rationality of the cascade combined generation, a cascade combined optimal model with the maximum generating capacity is established, and solving the model by the modified GA-POA method. It provides a useful reference for the joint development of cascade hydro-power stations in large river basins. The typical annual runoff data are selected to calculate the difference between the calculated results under different representative years. The results show that the cascade operation of cascaded hydro-power stations can significantly increase the overall power generation of cascade and ease the flood risk caused by concentration of flood season.

Download & links

Article (PDF, 1192 KB)

How to cite

How to cite.

1 Introduction

As more and more large and medium hydro-power stations are put into use in our country, the joint dispatching of cascaded hydro-power plants has been getting more and more widespread attention. In order to encourage all hydro-power stations in cascade hydro-power stations to actively participate in the joint dispatch in order to maximize the benefits, the hydro-power industry advocates the implementation of “Cascade, rolling, integrated” mode of operation (Xu, 2015; He, 2014; Zhou, 2016). In the joint operation of cascade hydro-power stations, the leading hydro-power station in the upper reaches has good regulating performance, which can greatly increase the power generation capacity of each downstream hydro-power station and has objective power generation compensation benefits (Li, 2016; Wang, 2014). So, reflecting the compensating function of power plants with good performance in cascade joint scheduling and solving the joint operation process by highly efficient and feasible algorithms mean very much.

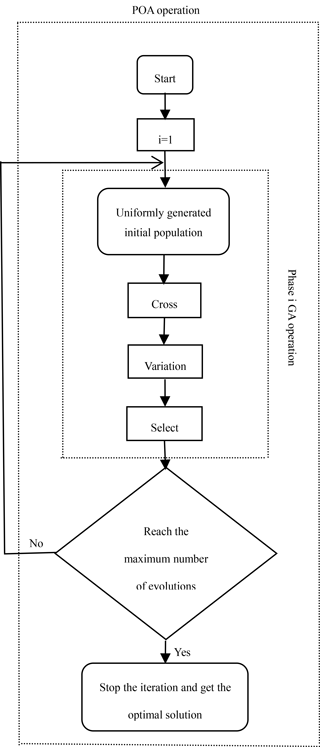
2 Modified GA-POA method

According to the idea of successive optimization, the T-stage optimization problem can be divided into several two-stage optimization sub-problems, while the sub-problem decision-making, using real-coded genetic algorithm to solve. Traditional genetic algorithms generate initial populations in a random way. However, randomized methods often fail to meet the requirements of “global distribution” of initial populations, which leads to their low representation and inefficiency. Based on this, the idea of uniform design is introduced into the generation of initial population of genetic algorithm to improve the initial population quality by increasing the uniform distribution of the initial population.

2.1 Coding method and initial population generation

Taking the water level of the library as a gene and coding with an integer, the population size is set as Size, $i = 1 \sim$ Size. The initial population is generated as follows:

\begin{array}{l} (1) & P_{i, t} = Z_{t, min} + 0.1 n \\ (2) & n = 10 \times (Z_{t, max} - Z_{t, min}) = 1, 2, \dots, size, \end{array}

where P_i,t is the integer coding of the i individual in the parent population at time t, $t = 1, 2, \dots, T + 1$ ; T is the number of scheduling period; $Z_{t, min}, Z_{t, max}$ is upper and lower water level.

2.2 Fitness function setting

The fitness function is used to evaluate the individual's advantages and disadvantages. In this paper, the size of power generation is mainly considered. When the system initial solution does not meet the minimum system output requirements, the penalty function is used to adjust. The objective function value:

\begin{matrix} (3) & ϕ (Z) = \sum_{t = 1}^{T} N_{t} \cdot Δ t + α \cdot min (\frac{N_{t} - N_{min}}{N_{min}}, 0), \end{matrix}

where T is Each time period; N_t is the output of the cascade at time t; N_min is system minimum output.

2.3 Cross operation

Using the single point crossover method, it is assumed that i₁ and i₂ cross at the time point:

\begin{matrix} (4) & P_{k, t}^{'} = \{\begin{cases} p_{i 1, t} t < time \\ p_{i 2, t} t \geq time \end{cases} P_{k + 1, t}^{'} = \{\begin{cases} p_{i 2, t} t < time \\ p_{i 1, t} t \geq time, \end{cases} \end{matrix}

where time $\in [1, 2, \dots, T + 1]$ , after crossing, a population P^′ of the same size as Size is formed.

2.4 Variation operation

Using random mutation, the gene P_y is controlled by the probability P_y, a new gene is generated at the mutation point:

\begin{matrix} (5) & P_{i, t}^{''} = \{\begin{cases} Z_{t, min} + (Z_{t, max} - Z_{t, min}) \cdot P_{y}^{'} P_{y}^{'} < P_{y} \\ P_{i, t} P_{y}^{'} \geq P_{y}, \end{cases} \end{matrix}

where P_y, $P_{y}^{'}$ are all random numbers distributed between [0, 1], mutation to population $P^{''}$ with the same population size of size.

2.5 Choose operation

The league method (Howson, 1975) was used to score a total of 3Size individuals in the parental group P, crossover groupP, and mutation group P. The scoring rules of individual i were as follows: size random individuals were randomly selected without duplication, and the adaptability of i exceeded that of the competition individuals counts Score as i score:

\begin{matrix} (6) & {Score}_{i} = Count {ϕ_{i} > ϕ_{j} |i, j \in Ω_{size}} . \end{matrix}

3Size individuals ranked according to the score, the highest score of Size individuals as a parent group into the next generation of evolution.

2.6 Evolution termination conditions

The evolution termination condition is to reach the maximum evolutionary algebra set in advance.

The multi-stage optimization problem in the progressive optimality algorithm is split into multiple two-stage sub-problems, and then the modified genetic algorithm is applied to the decision of the sub-problems. The modified GA-POA method solving flowchart is shown as Fig. 1.

https://www.proc-iahs.net/379/199/2018/piahs-379-199-2018-f01

Figure 1The modified GA-POA method solving flowchart.

Download

3 Mid and Long-Term Optimize Scheduling of Cascade Hydro-power Stations

3.1 The objective function

Model to maximize the power generation as the optimization goal, the mathematical description of:

\begin{matrix} (7) & max F = \sum_{i = 1}^{n} \sum_{j = 1}^{T} N_{i j} Δ t, \end{matrix}

where F is the goal of optimal scheduling is the total power generation of all stations in the cascade throughout the entire scheduling period; n is the number of reservoirs; T is scheduling period; N_ij is the i reservoir's output of j period; Δt is Time interval.

3.2 Restrictions

3.2.1 Water balance constraints

\begin{matrix} (8) & V_{t + 1} - V_{t} = (Q_{t} - q_{t}) \cdot Δ t, \end{matrix}

where $V_{t}, V_{t + 1}$ is the beginning and the end of the reservoir's storage capacity of t period;

Q_t, q_t is the average inflow and the average outflow.

3.2.2 Water level constraints

\begin{matrix} (9) & Z_{min} < Z_{t} < Z_{max}, \end{matrix}

where Z_max, Z_min is the reservoir's upper and lower water level of t period.

3.2.3 Output constraint

\begin{matrix} (10) & N_{min} < N_{t} < N_{max}, \end{matrix}

where N_max, N_min is the reservoir's upper and lower output.

3.2.4 Discharge flow constraints

\begin{matrix} (11) & q_{min} < q_{t} < q_{max}, \end{matrix}

where q_max, q_min is the reservoir's upper and lower outflow.

3.2.5 Hydraulic equation

\begin{matrix} (12) & I_{i, l} = q_{i - 1, l} + Q_{q j, l} - Q_{k s, l}, \end{matrix}

where I_i,l is the reservoir i^′s inflow of the l period; $q_{i - 1, l}$ is the reservoir i−1's outflow of the l period; Q_qj,l, Q_ks,l is the interval flow and the loss flow of the l period.

3.2.6 Non-negative conditional constraints

All of the above variables satisfy the non-negative condition.

3.3 Output and power generation

\begin{array}{l} (13) & N = K Q \cdot (H - Δ H) \\ (14) & Δ H = θ \cdot Q^{2} \\ (15) & E = N \cdot t, \end{array}

where K is output coefficient; Q is used flow; H is net head; ΔH is head loss; θ is coefficient of head loss; t is time; N,E is the output and power generation of hydro-power station.

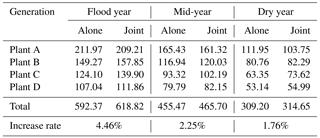
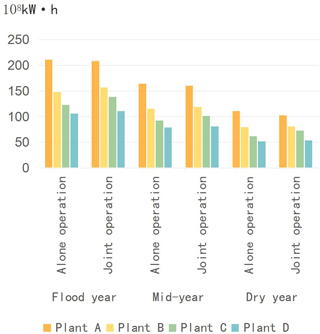
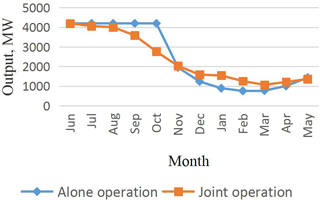
4 Case study

In this study, an example is given to four hydro-power stations in a river basin cascade in China, which are represented by A, B, C and D. Among them, A is the leading power plant with huge storage capacity and significant power generation benefit which has not been completed and put into production. The adjustment capacity of B, C and D is small, and the runoff data used in this study is the monthly typical runoff which are regarded as run-of-run power plants. In this study, population size = 200, maximum iteration generation = 300, crossover time = 3 and mutation probability = 0.03. Solving the model by the established modified GA-POA method with C $+ +$ programming language, the cascade power generation under different representative years are shown as Table 1 and Fig. 2.

Table 1Cascade power generation 10⁸ kW h.

Download Print Version | Download XLSX

https://www.proc-iahs.net/379/199/2018/piahs-379-199-2018-f02

Figure 2Cascade power generation.

Download

When cascade hydro-power station is operated in combination, the leading hydro-power station can effectively increase the power generation of the downstream hydro-power plants during the dry period, and the total generating capacity of the hydro-power station increases significantly. The power generation of joint operation growth by 4.46 % in flood year, 2.25 % in mid-year and 1.76 % in dry year than alone operation. The compensatory benefits meet the requirements of Flood Year > Mid-Year > Dry Year.

The joint operation can significantly improve the overall power generation of the cascade. When the water inflow is small, the joint operation has a greater significant. The upstream power station compensates the power plants of the downstream power stations and improves the output of the dry season and the seasonal power generation. It can also ease the flood risk caused by concentration of flood season. This will help mobilize the enthusiasm of the leading hydro-power station and downstream hydro-power stations to participate in the joint cascade scheduling and achieve the goal of joint operation, which bring the maximum benefit in the basin.

The monthly output process of each station in flood year when it is operated independently and jointly is shown as Figs. 3 to 6. When each station of cascades operates independently, the output of the power plant fluctuates greatly. The specific performance is that when in the flood season, the output is large; when in the dry season, the output is small.

https://www.proc-iahs.net/379/199/2018/piahs-379-199-2018-f03

Figure 3The output of plant A.

Download

https://www.proc-iahs.net/379/199/2018/piahs-379-199-2018-f04

Figure 4The output of plant B.

Download

https://www.proc-iahs.net/379/199/2018/piahs-379-199-2018-f05

Figure 5The output of plant C.

Download

https://www.proc-iahs.net/379/199/2018/piahs-379-199-2018-f06

Figure 6The output of plant D.

Download

When the water supply is reduced rapidly in some months, there are efforts to make a sharp turn; when the cascade power plants are jointly operated, the power plant output process is relatively gradual. Due to the regulation and storage of the leading power station, the output of the power plant during the flood season is smaller than that of the power station alone. In the dry season, the power plant output is greater than when the power station is operated alone. Output, the overall change is smaller than that of each power station when it is running alone, and the leading power station has a significant effect on the adjustment of the steps.

5 Conclusion

In this paper, the long-term optimal scheduling model is established, and the modified GA-POA method is proposed to solve the model by C $+ +$ programming. This model is applied to cascade reservoirs in a river basin in China, which achieved good results. The study provides a beneficial reference for the joint development of large-scale cascaded hydro-power stations.

Data availability

The data used in this paper are provided by the reservoir management departments, which can not be provided externally because the data are confidential.

Competing interests

The authors declare that they have no conflict of interest.

Special issue statement

This article is part of the special issue “Innovative water resources management – understanding and balancing interactions between humankind and nature”. It is a result of the 8th International Water Resources Management Conference of ICWRS, Beijing, China, 13–15 June 2018.

Acknowledgements

This study was financially supported by National Key Projects of China “Water resources efficient development and utilization” (2017YFC0405900, 2016YFC0402208, 2016YFC0401903) and National Natural Science Foundation of China (No.51641901). The author would like to give special thanks to anonymous reviewers.

Edited by: Yangbo Chen
Reviewed by: two anonymous referees

References

He, X., Wu, Y., and Jiang, G.: Profit allocation model of supply network based on revised Shapely value, Soft Science, 28, 70–73, 2014.

Howson, H. R. and Sancho, N. G. F.: A new algorithm for the solution of multi-state dynamic programming problems, Math. Program., 8, 104–106, 1975.

Li, Y., Zhou, J., Zhang, S., Huang, C., and Yan, D.: Combined dispatching chart of cascade hydropower stations on Yalong river, Jinsha river and Yangtze river, Journal of Hydroelectric Engineering, 35, 32–40, 2016.

Wang, Y., Guo, S., Zhou, Y., Hong, X., Hu, T., and Liu, D.: Uncertain analysis of long-term generation optimal operation for reservoirs, Water Resources and Power, 32, 61–65, 2014.

Xu, W.: Research on some issues in the joint optimal operation of cascaded reservoirs between Long yang xia and Liu jia xia, Tsinghua University, 2015.

Zhou, B.: Research on compensative operation of two-reservoirs and multi-cascaded hydropower plants, Da Lian University of Technology, 2016.