the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Impact of possible climate changes on river runoff under different natural conditions
Olga N. Nasonova
Evgeny E. Kovalev
Georgy V. Ayzel
The present study was carried out within the framework of the International Inter-Sectoral Impact Model Intercomparison Project (ISI-MIP) for 11 large river basins located in different continents of the globe under a wide variety of natural conditions. The aim of the study was to investigate possible changes in various characteristics of annual river runoff (mean values, standard deviations, frequency of extreme annual runoff) up to 2100 on the basis of application of the land surface model SWAP and meteorological projections simulated by five General Circulation Models (GCMs) according to four RCP scenarios. Analysis of the obtained results has shown that changes in climatic runoff are different (both in magnitude and sign) for the river basins located in different regions of the planet due to differences in natural (primarily climatic) conditions. The climatic elasticities of river runoff to changes in air temperature and precipitation were estimated that makes it possible, as the first approximation, to project changes in climatic values of annual runoff, using the projected changes in mean annual air temperature and annual precipitation for the river basins. It was found that for most rivers under study, the frequency of occurrence of extreme runoff values increases. This is true both for extremely high runoff (when the projected climatic runoff increases) and for extremely low values (when the projected climatic runoff decreases).
In the reports of the IPCC (Intergovernmental Panel on Climate Change, 2001, 2014), there are estimates of the increment in the mean annual air temperature and annual precipitation both for the entire globe and for various regions of the planet by the end of the 21st century. They show that for the past 100 years the global values of air temperature and precipitation have increased, respectively, by 0.6 ∘C and 2 % with large differences between the continents (IPCC, 2001). These climatic changes cause changes in characteristics of hydrological regime in different regions of the world. Investigation of possible changes in hydrological characteristics of various objects is an urgent problem in the environmental sciences.
In 2013, the International Inter-Sectoral Impact Model Intercomparison Project (ISI-MIP) (Warszawski et al., 2013) was launched. Its Water Sector was aimed at validation and improvement of hydrological models on regional and global scales and application of the models for hydrological projections of possible changes in water resources due to expected climatic changes. The present work was carried out within the framework of the ISI-MIP2 and its purpose was to study possible changes in characteristics of runoff from 11 large river basins (located on different continents under different natural conditions) by the end of 21st century caused by projected changes of climate. Similar large-scale multi-basin modelling studies were performed by nine hydrological models participating in the ISI-MIP (Krysanova and Hattermann, 2017). Here, in contrast to the mentioned paper, the Land Surface Model (LSM) SWAP (Soil Water-Atmoshere-Plants) (Gusev and Nasonova, 2010), rather than a hydrological model, is used as a main calculational tool.
Changes in such characteristics of river runoff as climatic runoff (runoff averaged over the period of 30–35 years), standard deviation of annual runoff within the specified climatic period, as well as a frequency of extreme values of annual runoff were calculated. The study of the two latter characteristics was motivated by the fact that increase in the frequency and magnitude of extreme climate events are stated in a number of publications (e.g., IPCC, 2001, 2014). As such, river flows are also expected to become more variable in the future, with more flash floods and lower minimum flows. This is confirmed by some fragmentary studies of changes in river runoff variability (e.g., Lin et al., 2008). The present paper is devoted to investigation of this statement by means of studying changes in standard deviation of annual runoff (caused by its natural variability) and frequency of annual runoff extreme values in the 21st century. In addition, the authors tried to generalize the calculated changes in climatic runoff in terms of the so-called climate elasticity of runoff in relation to changes in climatic values of air temperature and precipitation.
Table 1River basins with their area; gauge stations with coordinates; averaged over 1971–2000 air temperature T and precipitation P; change in the probability of extremely high runoff due to climate change (in accordance with RCP scenarios). The values of T and P are taken from (Krysanova and Hattermann, 2017); F3 is the probability of extremely high runoff for the period P3, F0 is the probability of extremely high runoff for the period P0, equaled to 2.5 %.
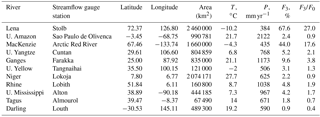
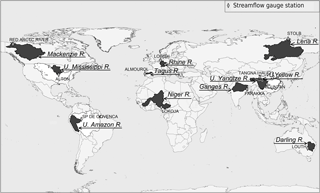
Objects of this study represent 11 large river basins located in different continents under different natural conditions: the Rhine and Tagus in Europe; the Ganges, Lena, Upper Yellow and Upper Yangtze in Asia, the Niger in Africa; the Mackenzie and Upper Mississippi in North America, the Upper Amazon in South America and the Darling in Australia (Fig. 1). The main characteristics of the selected river basins are given in Table 1.
The basins were schematized as a set of regular grid cells with a spatial resolution 0.5∘ × 0.5∘ in latitude and longitude connected by a river network (Gusev et al., 2017b).
3.1 SWAP model
The main tool for the present study is the SWAP model developed in the Institute of Water Problems of the Russian Academy of Sciences (Gusev and Nasonova, 1998, 2010). It is a physically-based land surface model with distributed parameters describing the processes of heat and water exchange in a soil – vegetation/snowpack – atmosphere system (SVAS). For a large-scale modelling, a selected river basin is divided into a number of calculational grid cells connected by a river network. The model simulations are performed for each calculational grid cell. After that the river routing model is used to simulate runoff at the basin outlet.
The SWAP model outputs are several dozens characteristics of thermal and water regimes of a river basin. However, here, only river runoff is considered. Model inputs include the land surface parameters and meteorological forcing data.
Different versions of the model SWAP were validated against observations including characteristics both related to energy balance or thermal regime of SVAS (sensible and latent heat fluxes, ground heat flux, net radiation, upward longwave and shortwave radiation, surface temperature, soil freezing and thawing depths) and related to hydrological cycle or water regime of SVAS (surface and total runoff from a catchment, river discharge, soil water storage in different layers, evapotranspiration, snow evaporation, intercepted precipitation, water table depth, snow density, snow depth and snow water equivalent, water yield of snow cover). The validations were performed for “point” experimental sites and for catchments and river basins of different areas (from 10−1 to 105 km2) on a long-term basis and under different natural conditions (from arid to humid and from non-frozen soils to permafrost). The results of validation (e.g., Boone et al., 2004; Grippa et al., 2017; Gusev et al., 2017a; Gusev and Nasonova, 2010; Nasonova et al., 2009) have shown that SWAP is able to reproduce annual and interannual dynamics of the mentioned characteristics fairly well.
3.2 Data
Here, for model calibration and validation, daily values of meteorological forcing data for the period of 1970–2001 to drive the SWAP model were derived from the Water and Global Change (WATCH) data set (Weedon et al., 2011) which was created on the base of the ERA-40 reanalysis product hybridized with monthly values of ground-based measurements (including air temperature, the number of days with precipitation, cloudiness and precipitation) taken from the Global Precipitation Climatology Center (GPCC) and the Climatic Research Unit (CRU of University of East England) data sets.
For hydrological projections, daily meteorological forcing data simulated by five General Circulation Models (GCMs: HadGEM2-ES, IPSL-CM5A-LR, MIROC-ESM-CHEM, GFDL-ESM2M, and NorESM1-M) for the period from 2006 to 2099 and for the four RCP (Representative Concentration Pathways) scenarios (RCP2.6, RCP4.5, RCP6.0 and RCP8.5) were used (Krysanova and Hattermann, 2017). These scenarios were designed for the 5th assessment report of IPCC (2014). The numbers in the names of scenarios correspond to increment of incoming radiation (in W m−2) in 2100 caused by increased greenhouse gas emission into the atmosphere as compared to a pre-industrial period. The larger numbers correspond to more aggressive anthropogenic scenarios due to increase in greenhouse gas emission and weak measures for its limitation. To increase the quality of hydrological projections a post-processing bias correction of meteorological projections to the WATCH data was performed within the framework of the ISI-MIP project.
The land surface parameters for each calculational grid cell were derived from the global ECOCLIMAP parameter data set (Champeaux et al., 2005) as described in Gusev et al. (2017b).
River runoff data for gauges listed in Table 1 were provided within the framework of the ISI-MIP project (see Huang et al., 2017 for details). Additional data for subbasins of the Lena and MacKenzie rivers were taken from the Global Runoff Data Centre (GRDC).
3.3 SWAP model calibration and validation
To improve the quality of hydrological calculations an automatic calibration of the most important model parameters based on the algorithm SCE-UA for searching the global extremum of an objective function (Duan et al., 1992) under the additional condition that the systematic error of runoff calculation cannot exceed 5 % (Nasonova et al., 2009) was carried out. The Nash and Sutcliffe coefficient of efficiency of simulating monthly river runoff was used as an objective function. For each river basin, the calibration was carried out for 8-year period (different for different rivers). Validation of the obtained optimal values of model parameters was carried out for the period of 1970–2001 and showed a satisfactory agreement between measured and simulated monthly runoff (Gusev et al., 2017b).
The obtained optimal values of model parameters were used for simulating daily runoff for the selected rivers by the SWAP model with meteorological forcing data from the above five GCMs. The runoff simulations were performed for two periods: historical P0 (1962–2005) and prognostic (2006–2099). The latter was divided into three parts: P1 (2006–2035), P2 (2036–2065) and P3 (2066–2099). For the prognostic period, runoff was simulated for the above four climate scenarios of the RCP family.
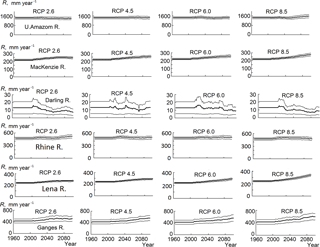
Figure 2Dynamics of multi-modal climatic river runoff (bold line) by the end of the 21st century in accordance with four RCP scenarios, as well as root mean square error of multi-model mean values (thin line).
4.1 Projections of changes in climatic river runoff
Some examples of the projected river runoff by the end of the 21st century are given in Fig. 2, where the dynamics of annual values of river runoff (obtained as a result of averaging of five runoff simulations with meteorological projections from five GCMs) for six river basins and four climate scenarios are shown. Here, for the historical period, river runoff was averaged over the period, while, for the prognostic periods, runoff values were calculated as 30-year moving averages to obtain an evolution of climatic runoff. Besides, Fig. 2 also shows the uncertainty of runoff projections caused by a scatter in GCMs' results and estimated as a root mean square error of an ensemble average.
The obtained results confirmed an expected conclusion that more aggressive scenarios lead to larger changes in river runoff from the selected basins, both in the positive and negative directions (for different basins). As to the relative error of climatic runoff (equaled to the absolute error divided by average runoff), it is the greatest for the Darling and Tagus rivers. It should be noted that according to Gusev et al. (2017b) these basins are also characterized by the greatest natural uncertainty of runoff caused by weather noise. For the northern rivers, Lena and Mackenzie, the relative error is the smallest that corresponds to the lowest values the natural uncertainty of river runoff from these basins (Gusev et al., 2017b). Apparently, for basins with the greatest amplitude of weather noise, the scatter of the dynamics of meteorological outputs from different GCMs is also the greatest, which, in turn, leads to greater differences between the values of river runoff calculated on their basis.
As to the changes in river runoff ΔR, they are evidently different (both in magnitude and sign) for basins in different regions of the planet due to differences in natural conditions, primarily climatic ones. We tried to generalize the obtained results, using the concept of climate elasticity of runoff.
Climate elasticity, introduced by Fu (1981), is used to determine the response of any variable (e.g., runoff) to climate change. For example, a precipitation elasticity of annual runoff of 2.2 suggests that annual runoff would increase with 22 % due to an increase in annual precipitation with 10 % (22 %∕10 % = 2.2). Negative elasticity means that changes of these two variables are of an opposite sign. The temperature elasticity (εT) and precipitation elasticity (εP) of runoff from each river basin was calculated as follows (Grijsen and Patel, 2014):
where R0, T0 and P0 are climatic values of annual runoff, air temperature and precipitation, respectively; ΔR, ΔT and ΔP are changes of these variables (here, P and R are in mm year−1, while T is in K).
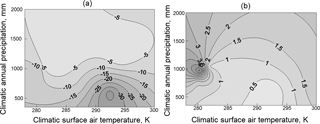
Figure 3Temperature elasticity of runoff εT (a) and precipitation elasticity of runoff εP (b). The elasticities are shown in isolines.
The calculated values of climate elasticities of runoff εT and εP for the selected basins were mapped, using the kriging procedure in the phase coordinates of T0 and P0 (Fig. 3). As can be seen in Fig. 3, the temperature elasticity of runoff εT is negative, because an increase in temperature raises evapotranspiration, leading to a decrease in runoff. The values of precipitation elasticity of runoff εP are positive, because an increase in precipitation results in an increment of runoff.
The values of climate elasticities in Fig. 3 give an opportunity to project, as the first approximation, changes in climatic annual river runoff, provided that projections of changes in mean annual air temperature and annual precipitation for a river basin are available.
4.2 Projections of changes in natural variability of river runoff
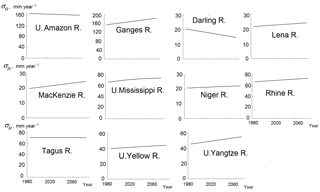
Now let us consider the second statistical moment – the standard deviation of annual river runoff σR within a 30-year range associated with a natural variability of runoff (caused by a weather noise). An error of estimation of the second moment is higher than that of the mean value of runoff and equals to approximately 13 % of σR for a sample of annual runoff values of length ≈ 30 (such an error is of the order of averaged over the basins change in σR in the 21st century). As such, to increase the accuracy of estimation of changes in runoff variability the values of σR obtained for each of the four climatic scenarios and five GCMs were averaged over the scenarios and GCMs for the periods P0, P1, P2 and P3. After that, their temporal dynamics was approximated by a linear or parabolic function. The error of the obtained value of σR did not exceed 2 %.
The results of estimation of the dynamics of σR in the 21st century obtained for different rivers are presented in Fig. 4. They show that for all rivers, with the exception of the Amazon, Darling and Tagus, the standard deviation of annual runoff σR increases by the end of the 21st century. The values of σR for the Amazon and Tagus rivers decrease, but insignificantly.
As to climatic values of annual runoff R, averaged over all climatic scenarios and GCMs, they have a noticeable downward trend only for the Tagus and Darling rivers. (Note, that the relative error of such estimates for different rivers is within the range of 0.5–1.5 %). For the Lena, Mackenzie and Ganges rivers, the climatic values of runoff demonstrate its apparent increase. The climatic runoff of the remaining rivers has an unremarkable growth by the end of the century (the Mississippi, Niger, and Rhine rivers) or does not change (the Amazon, Yellow and Yangtze rivers).
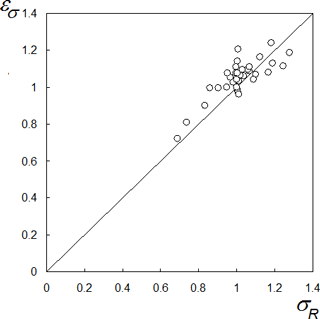
Figure 5 shows the relationship (for the climatic periods P1, P2 and P3 and for 11 rivers) between the relative standard deviation of annual runoff from its climatic value (where pr means any of prognostic periods: P1, P2 or P3; σR,pr and σR,P0 are standard deviations of annual runoff R for any of the prognostic period pr and for the historical period P0, respectively) and the relative value of climatic runoff . It is seen that, in the first approximation (with a coefficient of correlation ≈ 0.8), the change in the relative standard deviation of annual runoff εσ is proportional to the change in the relative climatic runoff εR. This means that for a particular river the variability of its annual runoff changes in proportion to changes in climatic runoff. Thus, as the first approximation, the value of σR,pr can be obtained on the basis of the following equation:
However, the obtained relation can be treated only very approximately, which is confirmed by the deviations of the circles in Fig. 5 from the line 1:1. This means that the ratio of deterministic and stochastic components in runoff of a particular river (Gusev et al., 2017b) can vary with climate change and, evidently, the value of σR,pr can be more accurately obtained by means of model sumulations.
4.3 Changing the frequency of extreme runoff
First of all, it should be noted that, here, runoff values that exceed quantile of annual runoff with 97.5 % probability for the historical period P0 are treated as extremely high annual river runoff, while runoff values that are lower than quantile of annual runoff with 2.5 % probability for the period P0 are considered as extremely low ones. Here, the main attention will be paid to changing the frequency of occurrence of extremely high runoff.
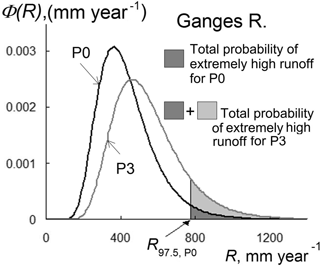
Figure 6Probability density Φ of annual runoff R for the Ganges River for the historical P0 and prognostic P3 periods. R97.5,P0 is the quantile of 97.5 % probability for the period P0 (the cut point for the extremely high runoff).
To solve this problem, we need to assess the impact of climate change on the distribution function of annual runoff. Different variants for approximating the distribution of river runoff on the basis of application of different distribution functions (the lognormal distribution, the Pearson distribution, the gamma distribution, the distribution by Kritskii and Menckel) are considered in Sikan (2007). An analysis of these variants in (Sikan, 2007) and the authors' own experience (Gusev et al., 2017a, b) shows that empirical distribution of annual runoff (at least within the range of probabilities from 0.025 to 0.975) can be satisfactorily approximated by the function of the two-parameter lognormal distribution. Application of more precise three-parameter functions of distribution in this case is not possible, because the accuracy of estimation of the third statistical moment, which is necessary to obtain the third parameter of the distribution function and reflects the degree of its asymmetry, is rather low (in contrast to the above-mentioned accuracy of the first two statistical moments) in the case of application of the samples of annual river runoff available for us. Therefore, in the present paper, a hypothesis about the possibility of approximation of the empirical distribution functions of annual runoff for the rivers under study by the two-parameter lognormal distribution is used.
The parameters of the lognormal distribution function of annual runoff for a particular river and time period (P0, …, P3) were derived from the empirical distribution of annual runoff calculated using forcing data from each GCM and for each RCP scenario. Then, these parameters were averaged over all GCMs and scenarios, and the obtained averages were used for constructing the final distribution function of runoff for each river and time period.
The obtained distribution functions of annual river runoff were used for estimating the change in the frequency of its extreme values due to possible climate change.
Figure 6 shows the calculated functions of distribution of annual runoff of the Ganges River for the historical P0 and prognostic P3 periods. The probability of appearance of extremely high runoff changes from 2.5 % for the historical period (the shaded area under the black curve) to 9.6 % for the prognostic period (the shaded area under the grey curve).
Similar calculations were carried out for all rivers under study. The results are shown in Table 1 (two last columns). Analysis of the results shows that changes in the frequency of occurrence of extremely high annual runoff fmax depend on the natural conditions of a particular river basin. For most rivers the frequency increases due to climate change (especially for rivers in the boreal zone). As a rule, for such rivers, according to the RCP scenarios, the climatic runoff also increases. For the U. Amazon, U. Yellow and Niger rivers, changes in fmax are within the error of its estimation (with accounting for errors of estimation of parameters of the approximating functions). For these rivers, changes in climatic runoff are also small. For the Darling and Tagus rivers, the frequency of extremely high runoff is noticeably reduced. And climatic runoff of these rivers also decreases. As to the frequency of extremely low annual runoff fmin, for the period P3, it is 4.1 and 1.2 times larger (for the Darling and Tagus rivers, respectively) than for the historical period P0, i.e. the frequency of the appearance of extremely low annual runoff is increasing.
For 11 large river basins, characterized by different natural conditions, possible changes in characteristics of river runoff caused by the expected climate changes according to climatic scenarios of the RCP-family up to 2100 are investigated. Changes in climatic runoff are different (both in magnitude and sign) for the river basins located in different regions of the planet due to differences in natural (primarily climatic) conditions. Climatic runoff has a noticeable downward trend only for the Tagus and Darling rivers. For the Lena, Mackenzie and Ganges rivers, the climatic values of runoff demonstrate its apparent increase. The climatic runoff of the remaining rivers has an unremarkable growth by the end of the century (the Mississippi, Niger, and Rhine rivers) or does not change (the Amazon, Yellow and Yangtze rivers).
As to variability of annual runoff, changes in the standard deviation of annual runoff from its climatic value, in the first (fairly coarse) approximation, are proportional to changes in climatic runoff. It is shown that for all rivers, with the exception of the Amazon, Darling and Tagus, the standard deviation of annual runoff σR increases by the end of the 21st century. The values of σR for the Amazon and Tagus rivers decrease, but insignificantly.
For most rivers under study, the frequency of occurrence of extreme runoff values increases. This is true both for extremely high runoff (when the projected climatic runoff increases) and for extremely low values (when the projected climatic runoff decreases).
Data were provided by ISI-MIP regional-scale water sector organizers, and by GRDC (the Global Runoff Data Centre, 56068 Koblenz, Germany).
The authors declare that they have no conflict of interest.
This article is part of the special issue “Innovative water resources management – understanding and balancing interactions between humankind and nature”. It is a result of the 8th International Water Resources Management Conference of ICWRS, Beijing, China, 13–15 June 2018.
The study was supported by the Russian Science Foundation (grant no.
14-17-00700 – Sect. 4.2 and 16-17-10039 all the other sections). We are
grateful to ISI-MIP regional-scale water sector organizers for providing
with data and materials, and to GRDC for providing discharge data.
Edited by: Zongxue Xu
Reviewed by: two anonymous referees
Boone, A., Habets, F., Noilhan, J., Clark, D., Dirmeyer, P., Fox, S., Gusev, Y., Haddeland, I., Koster, R., Lohmann, D., Mahanama, S., Mitchell, K., Nasonova, O., Niu, G.-Y., Pitman, A., Polcher, J., Shmakin, A. B., Tanaka, K., van den Hurk, B., Verant, S., Verseghy, D., Viterbo, P., and Yang, Z.-L.: The Rhone-aggregation land surface scheme intercomparison project: An overview, J. Climate, 17, 187–208, 2004.
Champeaux, J. L., Masson, V., and Chauvin, F.: ECOCLIMAP: a global database of land surface parameters at 1 km resolution, Meteorol. Appl., 12, 29–32, 2005.
Duan, Q., Sorooshian, S., and Gupta, V. K.: Effective and efficient global optimization for conceptual rainfall runoff models, Water Resour. Res., 28, 1015–1031, 1992.
Fu, B.: On the calculation of the evaporation from land surface, Sci. Atmos. Sin., 5, 23–31, 1981.
Grijsen, J. and Patel, H.: Understanding the impact of climate change on hydropower: the case of Cameroon – climate risk assessment for hydropower generation in Cameroon, World Bank Group, AFTEG, Washington DC, Report 87913, 151, 2014.
Grippa, M., Kergoat, L., Boone, A., Peugeot, C., Demarty, J., Cappelaere, B., Gal, L., Hiernaux, P., Mougin, E., Ducharne, A., Dutra, E., Anderson, M., Hain, C., Ait-Mesbah, S., Balsamo, G., Boussetta, S., Chaffard, V., Chan, E., Cohard, JM, Favot, F., Gascon, T., Gascoin, S., Getirana, A., Galle, S., Gosset, M., Guichard, F., Gusev, Y., Harris, P., He, X., Hector, B., Kaptue, A., Kazuaki, Y., Kotsuki, S., Kim, H., Kumar, S., Lebel, T., M-H, Lo, Mahanama, S., Magand, C., Maignan, F., Mamadou, O., Nasonova, O., Oki, T., Ottlé, C., Pellarin, T., Pierre, C., Richard, A., Roujean, J.-L., Polcher, J., Quantin, G., Séguis, L., Shmakin, A., Sokratov, V., Tanaka, K., Turkov, D., Velluet, C., Verseghy, D., and Vischel, T.: Modelling surface runoff and water fluxes over contrasted soils in pastoral Sahel: evaluation of the ALMIP2 land surface models over the Gourma region in Mali, J. Hydrometeorol., 18, 1847–1866, 2017.
Gusev, E. M. and Nasonova, O. N.: Modelling heat and water exchange between the land surface and the atmosphere, Nauka, Moscow, 2010.
Gusev, Y. M. and Nasonova, O. N.: The Land Surface Parameterization scheme SWAP: description and partial validation, Global Planet. Change, 19, 63–86, 1998.
Gusev, Y. M., Semenov, V. A., Nasonova, O. N., and Kovalev, E. E.: Weather noise impact on the uncertainty of simulated water balance components of river basins, Hydrol. Sci. J., 62, 1181–1199, 2017a.
Gusev, Y. M., Nasonova, O. N., Kovalev, E. E., and Aizel, G. V.: Modelling river runoff and estimating its weather-related uncertainty for 11 large-scale rivers located in different regions of the globe, Hydrol. Res., https://doi.org/10.2166/nh.2017.015, in press, 2017b.
Huang, S., Kumar, R., Florke, M., Yang, T., Hundecha, Y., Kraft, P., Gao, C., Gelfan, A., Liersch, S., Lobanova, A., Strauch, M., Ogtrop, F., Reinhardt, J., Haberlandt, U., and Krysanova, V.: Evaluation of an ensemble of regional hydrological models in 12 large-scale river basins worldwide, Climatic Change, 141, 381–397, 2017.
Intergovernmental Panel on Climate Change (IPCC): Climate Change 2001: The scientific basis, Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, UK and New York, 881 pp., 2001.
Intergovernmental Panel on Climate Change (IPCC): Climate Change 2014: Synthesis Report, Contribution of Working Groups I, II and III to the Fifh Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Core Writing Team, Pachauri, R. K., and Meyer, L. A., IPCC, Geneva, Switzerland, 151 pp., 2014.
Krysanova, V. and Hattermann, F. F.: Intercomparison of climate change impacts in 12 large river basins: overview of methods and summary of results, Climatic Change, 141, 363–379, 2017.
Lin, X., Zhang, Y., Yao, Z., Gong, T., Wang, H., Chu, D., Liu, L., and Zhang, F.: The trend on runoff variations in the Lhasa River Basin, J. Geogr. Sci., 18, 95–106, doi.org/10.1007/s11442-008-0095-4, 2008.
Nasonova, O. N., Gusev, Y. M., and Kovalev, Y. E.: Investigating the ability of a land surface model to simulate streamflow with the accuracy of hydrological models: A case study using MOPEX materials, J. Hydrometeorol., 10, 1128–1150, 2009.
Warszawski, L., Frieler, K., Huber, V., Piontek, F., Serdeczny, O., and Schewe, J.: The inter-sectoral impact model intercomparison project (ISI–MIP): project framework, P. Natl. Acad. Sci. USA, 111, 3228–3232, 2013.
Weedon, G. P., Gomes, S., Viterbo, P., Shuttleworth, W. J., Blyth, E., Österle, H., Adam, J. C., Bellouin, O., and Best, M.: Creation of the WATCH Forcing Data and its use to assess global and regional reference crop evaporation over land during the twentieth century, J. Hydrometeol., 12, 823–848, 2011.
Sikan, A. V.: Methods of statistical processing of hydrometeorological information, Textbook, Speciality “Hydrology”, RGGMU, St. Petersburg, 2007.