the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Temporal and spatial variation of hydrological condition in the Ziwu River Basin of the Han River in China
Ziyan Li
Qiang Huang
Shuai Zhou
Mu Lin
The middle route of South-To-North Water Diversion in China transfers water from the Han River and Han-To-Wei Water Diversion project of Shaanxi Province will transfer water from the Ziwu River, which is a tributary of the Han River. In order to gain a better understanding of future changes in the hydrological conditions within the Ziwu River basin, a Mann–Kendall (M–K) trend analysis is coupled with a persistence analysis using the rescaled range analysis (R/S) method. The future change in the hydrological characteristics of the Ziwu River basin is obtained by analysing the change of meteorological factors. The results show that, the future precipitation and potential evaporation are seasonal, and the spatial variation is significant. The proportion of basin area where the spring, summer, autumn and winter precipitation is predicted to continue increase is 0.00, 100.00, 19.00 and 16.00 %, meanwhile, the proportion of basin area that will continue to decrease in the future respectively will be 100.00, 0.00, 81.00 and 74.00 %.The future potential evapotranspiration of the four seasons in the basin shows a decreasing trend. The future water supply situation in the spring and autumn of the Ziwu River basin will degrade, and the future water supply situation in the summer and winter will improve. In addition, the areas with the same water supply situation are relatively concentrated. The results will provide scientific basis for the planning and management of river basin water resources and socio-hydrological processes analysis.
According to the Intergovernmental Panel Climate Change report (IPCC, 2014), climate change acts as the driving factor of water cycle in hydrological processes and precipitation and evaporation are the main climatic factors affecting fresh water resources. The interaction of climate change with other factors has had irreversible negative impacts on the ecological and hydrological cycle of the basin. The Ziwu River basin, which is a tributary of the upper reach of the Han River, is located in the warm humid and semi-humid climate region of the north subtropics. The precipitation in the river basin changes significantly between seasons. Summer has the most precipitation, accounting for 46 % of the annual precipitation averaged across the basin, and winter the least at about 3 % (Zhang and Zhang, 2004). The seasonal variation of precipitation will inevitably lead to differences in the temporal and spatial distribution of hydrological conditions, and therefore it is very important to study the temporal and spatial variation of hydrological condition in the basin of the climate change.
In the context of the growing shortage of water resources in the world, the impact of water resources in the changing environment has received widespread attention (Xia et al., 2015). In view of the study of changing environment, domestic and foreign scholars mainly study the characteristics of river basin climate element change (Zhu et al., 2005; Chebana et al., 2013; Ma et al., 2012). Qiu et al. (2003) used the 20 cm caliber evaporator data from 123 meteorological stations in the Yellow River basin and its surrounding areas from 1961 to 2000 to analyse the climatic trend of pan evaporation. The study found that the average annual temperature of the Yellow River basin increased by 0.6 ∘C during the period from 1960 to 2000, but the evaporation of the evaporating pan showed a decreasing trend, especially during spring and summer. Shi et al. (2006) established an exponential formula for estimating evaporation capacity according to the relationship between evaporation capacity and temperature in the Yellow River basin, to analyse the influence of temperature change on the evaporation capacity. The results showed that the basin evaporation capacity increased by 5.0–7.0 % when the temperature increased by 1 ∘C.
Generally, the methods of M–K mutation point and trend test, rescaled range analysis (R/S) and wavelet analysis are used to analyse the change characteristics of climate elements in the basin (Rzeszotko, 2012; Wallis and Matalas, 1970). For the trend analysis of meteorological elements, most scholars adopt the mature Mann–Kendall and rescaled range analysis method (Whitfield and Hendrata, 2006; Polemio et al., 2008). Ling et al. (2011) tested the temperature, precipitation and evaporation in the Manas River basin for nearly 52 years and used the R/S analysis method to predict the future trend. The results showed that the temperature and precipitation increased significantly from 1956 to 2007 and the evaporation is significantly reduced. Using the R/S analysis method to test for long-range temporal dependence in the data, Dinh and Molnr (1999) showed that the R/S analysis method has good robustness. It can be seen that in the time series, a trend has a significant influence on the estimated Hurst value. Using global inventory modeling and mapping studies (GIMMS) data, Bisognin and Lopes (2007) selected three periods to study seasonal vegetation trends, resulting in a nonlinear variation in vegetation changes caused by drought. Zhang et al. (2012) used R/S analysis to predict the dynamic trend of future groundwater level in the Loess Platform area of Xingping City. The results show that the annual precipitation in Xingping decreases slightly, and the quantity of irrigation water decreases significantly, which is consistent with the dynamic trend of groundwater level change in the same period. Previous studies have mostly analyzed the temporal and spatial evolution characteristics of the meteorological elements in the basin under the historical conditions, while there are relatively fewer studies of the impact of meteorological factors on the future hydrological conditions of the basin.
In summary, this paper takes the Ziwu River basin of the upper reach of the Han River as the study area. In order to gain a better understanding of the temporal and spatial distribution of future water resources changes in the Ziwu River basin, the Mann–Kendall (M–K) trend analysis method is combined with a persistence analysis using the rescaled range analysis (R/S) method in this study. The temporal and spatial variation characteristics of precipitation and evaporation trends and persistence in future is obtained by setting indicators set for determining the future change of regional meteorological elements and setting situations of regional future water supply. This will provide scientific basis for the planning and management of river basin water resources and socio-hydrological processes analysis.
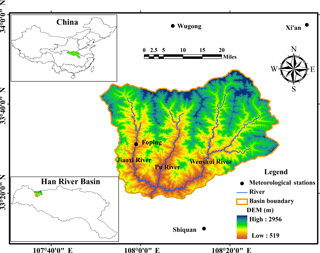
The Ziwu River, which is a tributary of the Han River, originates in the south of the Qinling Mountain of Gangtie Town, Ningshan County, flows through Ningshan County, Shiquan County, Yangxian County and Xixiang County, and enters into Han River at Xixiang County. In Fig. 1, the Wenshui River above Sanhekou reservoir is 106 km, the Jiaoxi River is 70 km and the Pu River is 58 km. The basin area is 3028 km2, and the altitude ranges from 360–2960 m. It is in the warm humid and semi-humid climate region of the north subtropics, where summer is warm and humid, winter is cold and dry and the spatial difference of seasonal precipitation in the basin is significant. The average annual temperature is between 7.7–15.7 ∘C and annual average precipitation is 900 mm.
In this paper, the precipitation and potential evapotranspiration data of the four meteorological stations in the Ziwu River basin from 1960 to 2013 are used and the potential evaporation data are calculated by the Penman–Monteith formula revised by the Food and Agricultural Organization (FAO). The Penman–Monteith formula is used to calculate potential evaporation data because it considered the influence of meteorological factors such as temperature, relative humidity, sunshine hours and wind speed and it is also a commonly used formula for calculating the potential evaporation in hydrological, meteorological and agriculture fields (Yang et al., 2012).
3.1 Mann–Kendall trend analysis
The nonparametric M–K test (Mann, 1945; Kendall, 1975) has been commonly used to assess the significance of monotonic trends in meteorological and hydrological data time series, but it can't predict the future trend of the sequence (Hamed, 2008). Suppose a set of hydro-meteorological time series X=(x1, x2, x3⋅, xn) (n is the number of variables in the sequence), and then establish the standard normal distribution statistic Z.
The M–K test statistic (S) is calculated in the following Eqs. (1) and (2):
where xi and xj are the data values at times i and j, n indicates the length of the data set. While a positive value of S indicates an increasing trend, a negative of S indicates a decreasing trend. The following expression, as an assumption, is used for the series where the data length n>10 and data are approximately normally distributed (variance (σ2=1) and mean (μ=0) value).
in this equation, P is the number of tied groups, and the summary sign (∑) indicates the summation over all tied groups. tk is the number of data values in the “Pth” group. If there are not the tied groups, this summary process can be ignored.
After the calculation of the variance of time series data with Eq. (3), the standard Z value is calculated according to the following Eq. (4).
the changing trend of judging the standard: (1) If the statistics Z is greater than 0, the past trend is increase, on the contrary, if the statistics Z is less than 0, the past trend is reduced; (2) if the statistics Z is greater than or equal to 1.96, the trend is increase significantly, on the contrary, if the statistics Z is less than or equal to −1.96, the trend is decrease significantly.
3.2 Hurst Exponent
The R/S analysis (Rescaled Range Analysis) is a statistical method proposed by Hurst, a British hydrologist in 1951 to deal with hydrologic time series from the Nile (Hurst, 1951). This method is used to quantitatively characterize the persistence or long-range dependency of a time series. The statistic Hurst exponent can well reveal the relationship between the future and past trends of the time series so that future trend changes can be predicted based on the past trends of the time series. Up until now, it has been widely applied to the qualitative prediction of meteorological and hydrology time series such as rainfall, evaporation and runoff. And the magnitude of the H value can be used to determine the strength of persistence and anti-persistence of future trend components (Feng et al., 2008). The Hurst index rating table is showed in Table 1. Although the H value can show the trend of change, it can't determine the actual historical trends. The Hurst exponent calculation process is as follows:
Suppose a set of hydro-meteorological time series {X(t)} (t is the number of variables in the sequence). For any positive integer (τ≥1), the mean value series ( is calculated in the following Eq. (5).
then the cumulative deviation can be calculated in the following Eq. (6).
The range R(τ) and standard deviation S(τ) are calculated in the following Eqs. (7) and (8) respectively.
Therefore, the Hurst exponent can be expressed by following Eq. (9).
where α is constant and H is the Hurst index.
Eventually, the Hurst exponent is calculated in the following Eq. (10). It can be obtained by logarithm of Eq. (9).
The criterion is as follows: if H value is greater than 0.50 and less than 1, the variables are positively correlated and the trend of future changes is consistent with the past; the H value is closer to 1, the persistence is stronger. If H value is greater than 0 and less than 0.50, the variables are negatively correlated and the trend of future changes is opposite to the past; the H value is closer to 0, the anti-persistence is stronger. If H value is equal to 0.50, the time series is random and future trends have nothing to do with the past.
3.3 Discriminant analysis of hydrological condition
Precipitation and evaporation are important links in the process of water cycle and also important indicators of the local hydrological conditions. Because the test method of Mann–Kendall and R/S are unable to independently obtain the past and future trends of hydrological sequences, this paper uses the method of Mann–Kendall test and R/S test coupled to determine the indicators set for determining the future change of regional meteorological elements, which are shown in Table 2.
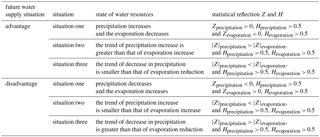
Regional hydrological conditions are greatly influenced by evaporation and precipitation under natural conditions. If one of the following three situations can happen, the regional water supply situation will improve in the future. In the situation one, the future regional precipitation increases and the evaporation decreases. In the situation two, the trend of precipitation increase is greater than that of evaporation increase. In the situation three, the trend of decrease in precipitation is smaller than that of evaporation reduction. If one of the following three situations can happen, the regional water supply situation will degrade in the future. In the situation one, the future regional precipitation decreases and the evaporation increases. In the situation two, the trend of precipitation increase is smaller than that of evaporation increase. In the situation three, the trend of decrease in precipitation is greater than that of evaporation reduction. Scientifically and reasonably evaluating the evolvement characteristics of the water supply situation in the future will have important practical significance for the sustainable development of the regional economy and society. This paper sets the situations of regional future water supply, which are seen in Table 3.
Whether the future water supply situation will be advantageous or disadvantageous depends on the relative differences in the change degree of precipitation and evaporation. This paper considers a total of six situations of advantageous (situation one, situation two and situation three) and disadvantageous (situation one, situation two and situation three) situations.
In summary, the advantageous/disadvantageous area for future water supply in the river basin is calculated as follows:
The Thiessen polygon method is used to calculate the area weights fi of basin features represented by the meteorological stations in the river basin and calculate the area represented by each station.
The Mann–Kendall analysis method and R/S analysis method is used to calculate the Z and H values of rainfall statistics at each station.
Based on the water supply evaluation indicators, the future water supply characteristics of the areas represented by each site are analysed.
Collect advantageous and disadvantageous sites for future water supply and calculate the area of advantageous or disadvantageous area for future water supply in the basin by combining the area weights of advantageous or disadvantageous sites calculated in step (1) with Eq. (11):
where F is the total area of the river basin and fi is the area weights of advantageous or disadvantageous area for future water supply.
4.1 Analysis of tendency and sustainability of precipitation change
4.1.1 Precipitation historical change trend
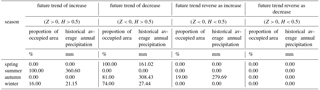
The Mann–Kendall nonparametric test method is used to calculate past trends of precipitation for all 4 weather stations considered in this study. The results shows that the proportion of sites with decreasing trend respectively in spring, summer, autumn and winter is 100.00, 0.00, 100.00 and 84.00 %, respectively, and the proportion of sites with increasing trend in spring, summer, autumn and winter is 0.00, 100.00, 0.00 and 16.00 %, respectively. It can be seen from historical trends that the supply of water in spring and autumn is in a form of harshness and the water supply in summer is in a good form.
4.1.2 Precipitation change sustainability
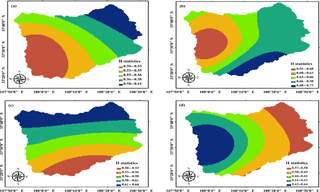
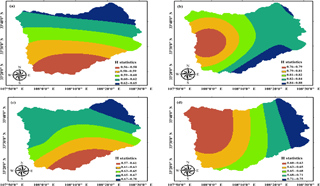
The precipitation H statistic value of each weather station is calculated by the R/S analysis method, and spatial interpolation is carried out by kriging interpolation method based on the ArcGIS environment. The result is shown in Fig. 2. According to Fig. 2, the H values of the four seasons are mainly concentrated in the range of 0.50–0.75 and the precipitation H value is significantly different in the spatial distribution. The spatial distribution trend of the H value in the four seasons is as follows: In spring, the H value of precipitation gradually increases from southwest to northeast, that is to say, the intensity of future sustainability gradually increases from southwest to northeast; In summer, the H value of precipitation is the smallest in the northwest local region and it is very large in the southeast part; In autumn, the H value of precipitation increases from south to north, that is to say, the intensity of future sustainability gradually increases from south to north; In winter, the H value of precipitation gradually increases from west to east, that is to say, the intensity of future sustainability gradually increases from west to east. Each season has a strong sustainability and regularity, which is conducive to the study of future water supply and development.
4.1.3 Precipitation trends in the future
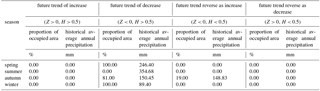
The results of the trend of future precipitation in the Ziwu River basin with time are shown in Table 4. The proportion of basin area where the spring, summer, autumn and winter precipitation is predicted to continue increase is 0.00, 100.00, 19.00 and 16.00 %, corresponding to the average annual precipitation of 0.00, 360.60, 279.69 and 21.15 mm, respectively; The proportion of basin area that will continue to decrease in the future respectively will be 100.00, 0.00, 81.00 and 74.00 %, corresponding to the average annual precipitation of 161.02, 0.00, 308.43 and 27.44 mm, respectively. The proportion of area where precipitation will be reversed in the future will be smaller in the seasonal scale.
4.2 Analysis of tendency and sustainability of potential evaporation change
4.2.1 Potential evaporation historical change trend
The Mann–Kendall nonparametric test method is used to calculate past trends of potential evaporation in all weather stations in the basin. In theory, the reduction of potential evaporation is conducive to the change of water supply at all seasons from poor to favorable trend.
4.2.2 Potential evaporation change sustainability
The potential evaporation H statistic value of each weather station was calculated by the R/S analysis method and spatial interpolation was carried out by kriging interpolation method based on the ArcGIS environment. The result is shown in Fig. 3. According to Fig. 3, the spatial distribution of potential evaporation H is significantly different. The potential evaporation in summer is the largest, even in some areas reached 0.88; it in winter take second place; and it in spring is the smallest. Each season has a strong sustainability and regularity, which is conducive to the study of future water supply and development.
4.2.3 Potential evaporation trends in the future
The results of a comprehensive analysis of potential evaporation past trends (Mann–Kendall test) and future sustainability (R/S test) are shown in Table 5. The results show that the potential evapotranspiration of the four seasons in the basin shows a decreasing trend. The historical potential evapotranspiration in spring, summer, autumn and winter respectively are 246.40, 354.68, 150.45 and 89.40 mm, which indicates that the basin will be humid in the future and is beneficial to the sustainable development of the local water resources.
4.3 Variation characteristics of future hydrological conditions in the basin
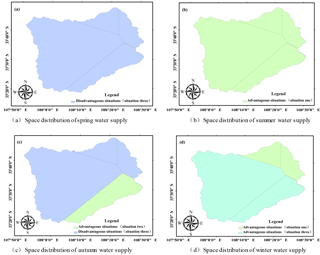
According to the trend of precipitation and evaporation in the future, the precipitation and evaporation in the basin have seasonal variation, which lays a good foundation for the study of the future hydrological conditions of the basin. Table 6 and Fig. 4 show that the future water supply situation of the basin is severe (disadvantageous) and good (advantageous) in regional spatial and temporal distribution.
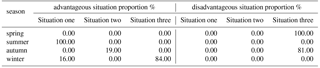
The results show that: the area of severe water supply in spring, summer, autumn and winter respectively are 100.00, 0.00, 81.00 and 0.00 %. The future of the water supply in the spring and autumn is predicted to be more limited than in the past. The trend of decreasing precipitation in spring and autumn is greater than that in potential evaporation, and most of the water supply in the autumn basin is severe excluding area which is 19 % in the southeast. These indicate that the future water supply is severe and are not conducive to the good development of regional hydrological conditions.
The area of water supply in spring, summer, autumn and winter good areas respectively account for 0.00, 100.00, 19.00 and 100.00 %. The summer water supply is situation one and the contradiction between supply and demand of water resources will be eased in the season; The water supply in autumn is situation two, which mainly distribute in some areas of the southeast of the basin; The water supply in winter are situation one and three. The trend of decreasing precipitation is less than that of potential evaporation in most areas of the river basin, and the contradiction between the future water supply in summer and winter will be alleviated.
To sum up, the water supply in the future will be severe in spring and autumn, and the water supply in the future will be good in summer and winter, especially in the summer with a good space for development which precipitation will increase and evaporation will decrease.
In this paper, the Mann–Kendall non-parametric test and R/S test methods were combined to analyse the historical trend and future trend of precipitation and potential evaporation in the river basin. After combining the characteristics of future hydrological conditions, the following conclusions are obtained:
The future precipitation and potential evaporation are seasonal, and the spatial variation is significant. In addition, the areas with the same water supply situation are relatively concentrated. The proportion of basin area where the spring, summer, autumn and winter precipitation is predicted to continue increase is 0.00, 100.00, 19.00 and 16.00 %, meanwhile, the proportion of basin area that will continue to decrease in the future respectively will be 100.00, 0.00, 81.00 and 74.00 %.The future potential evapotranspiration of the four seasons in the basin shows a decreasing trend.
The area of water supply in spring, summer, autumn and winter good areas respectively account for 0.00, 100.00, 19.00 and 100.00 % and the area of severe water supply in spring, summer, autumn and winter respectively are 100.00, 0.00, 81.00 and 0.00 %. The future water supply in the spring and autumn of the Ziwu River basin will be severe, and the future water supply in the summer and winter will be better, especially in the summer.
The meteorological data in the paper are provided by China Meteorological Data Service Center, from their web site at http://data.cma.cn/en.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Innovative water resources management – understanding and balancing interactions between humankind and nature”. It is a result of the 8th International Water Resources Management Conference of ICWRS, Beijing, China, 13–15 June 2018.
This work was partially supported by National Key R&D Program of China
(2017YFC0405900) and National Natural Science Foundation of China (NSFC)
(Grant No. 51779203, 51609270, 41330858). Funding was also provided by the
Basic Research Plan of Natural Science of Shaanxi Province (2016JQ5105). The
authors would like to thank Andreas Schumann and the anonymous reviewers for
their comments to improve the paper.
Edited by: Andreas Schumann
Reviewed by: two anonymous referees
Bisognin, C. and Lopes, S. R. C.: Estimating and forecasting the long-memory parameter in the presence of periodicity, J. Forecast., 26, 405–427, https://doi.org/10.1002/for.1030, 2007.
Chebana, F., Ouarda, T. B. M. J., and Duong, T. C.: Testing for multivariate trends in hydrologic frequency analysis, J. Hydrol., 486, 519–530, https://doi.org/10.1016/j.jhydrol.2013.01.007, 2013.
China Meteorological Data Service Center: available at: http://data.cma.cn/en (last access: 21 May 2017), 2017.
Dang, T. D. and Molnr, S.: On the effects of non-stationarity in long-range dependence tests, Periodica Polytechnica Ser.el.eng, 43, 227–250, 1999.
Feng, X. L., Feng, Z. L., Luo, L. C., Qin, L. L., and Lin, P.: R/S analysis and Hurst exponential test of climate change trend of Qinghai-Tibet Plateau, J. Arid Land Geogr., 31, 175–181, https://doi.org/10.13826/j.cnki.cn65-1103/x.2008.02.002, 2008.
Hamed, K. H.: Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis, J. Hydrol., 349, 350–363, https://doi.org/10.1016/j.jhydrol.2007.11.009, 2008.
Hurst, H. E.: Long term storage capacities of reservoirs, Trans. Am. Soc. Civil Eng., 116, 776–808, 1951.
IPCC: Synthesis Report, Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Core Writing Team, Pachauri, R. K., and Meyer, L. A., Geneva, Switzerland, 151 pp., 2014.
Kendall, M. G.: Rank Correlation Methods, M, 4th ed, Charles Griffin, London, 1975.
Ling, H. B., Xu, H. L., Zhang, Q. Q., and Shi, W.: Climate Change in the Manas River Basin, Xinjiang during 1956–2007, J. Glaciol. Geocryol., 33, 64–71, 2011.
Ma, X. N., Zhang, M. J., Huang, X. Y., Ma, Q., and Pan, S. K.: Characteristics of climate change and future trend in the upper Yellow River basin from 1960 to 2008, Arid Land Resour. Environ., 26, 17–23, https://doi.org/10.13448/j.cnki.jalre.2012.06.029, 2012.
Mann, H. B.: Nonparametric tests against trend, J. Econometrica, 13, 245–259, 1945.
Polemio, M., Casarano, D., Dragoni, W., and Sukhija, B. S.: Climate change, drought and groundwater availability in southern Italy, Geol. Soc. London Special Pub., 288, 39–51, https://doi.org/10.1144/SP288.4, 2008.
Qiu, X. F., Liu, C. M., and Zeng, Y.: Changes of pan evaporation in the recent 40 years over the Yellow River Basin, J. Nat. Res., 18, 437–442, 2003.
Rzeszotko, Z.: Estimation of the Hurst exponent for market indices by use of rescaled range method and CAS Mathematica. Case study: S&P500, Electro. J. Mathe. Technol., 6, 256–267, 2012.
Shi, Z. H., Wang, G. Q., Yv, H., Jiang, Y. F., Jin, X. A., and Li, H. B.: Impact of Temperature change on Potential Evaporation in Yellow River Basin, Meteorol. J. of Henan, 1, 31–32, https://doi.org/10.3969/j.issn.1673-7148.2006.01.015, 2006.
Wallis, J. R. and Matalas, N. C.: Small Sample Properties of H and K Estimators of the Hurst Coefficient h, Water Resour. Res., 6, 1583–1594, 1970.
Whitfield, P. H. and Hendrata, M.: Assessing Detectability of Change in Low Flows in Future Climates from Stage Discharge Measurements, Canadian Water Res. J., 31, 1–12, https://doi.org/10.4296/cwrj3101001, 2006.
Xia, J., Shi, W., Luo, X., Hong, S., Ning, L., and Chiristopher, J. G.: Revisions on water resources vulnerability and adaption measures under climate change, J. Adv. Water Sci., 26, 279–286, https://doi.org/10.14042/j.cnki.32.1309.2015.02.019, 2015.
Yang, H. B., Lv, H. F., Yang, D. W., and Hu, Q. F.: Seasonality of precipitation and potential evaporation and its impact on catchment water-energy balance, J. Hydroelec. Eng., 31, 54–59, 2012.
Zhang, K. and Zhang, S. T.: Analyses of “02.6” Ziwu River Extraordinary Flood in South of Shaanxi Province, J. Water Resour. Archit. Eng., 2, 54–56, 2004.
Zhang, Y. Q., Hu, W., and Liu, J. M.: Groundwater level regime variation trend on basis of rescaled range analysis, J. Central South Univ., 43, 4912–4916, 2012.
Zhu, H. H., Qin, D. Y., Zhou, Z. H., Yan, D. H., and Yang, G. Y.: Study on Precipitation Evolution Law of the Yellow River Basin, J. Yellow River, 27, 21–24, 2005.