Three-dimensional fully coupled study of groundwater seepage and soil deformation under the action of cyclic pumping and recharge
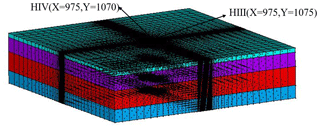
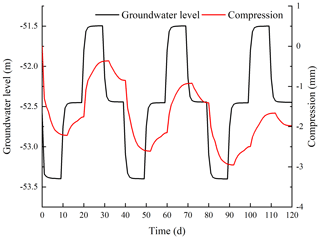
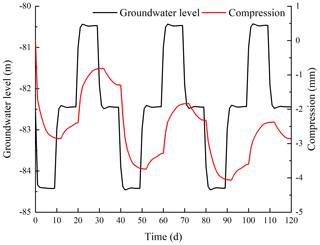
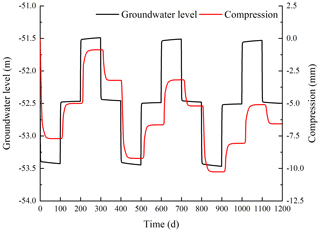
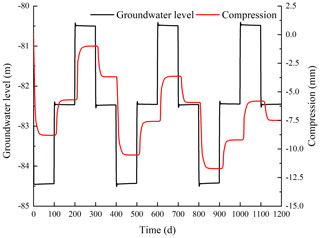
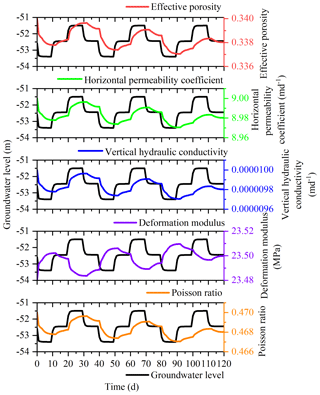
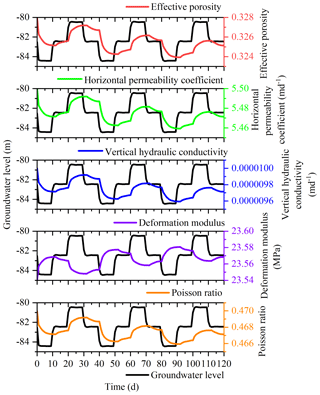
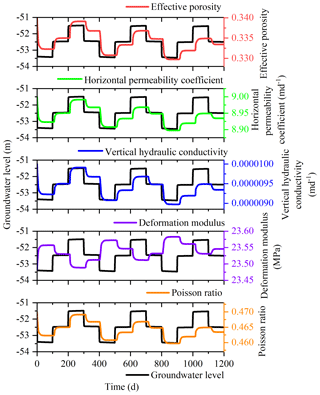
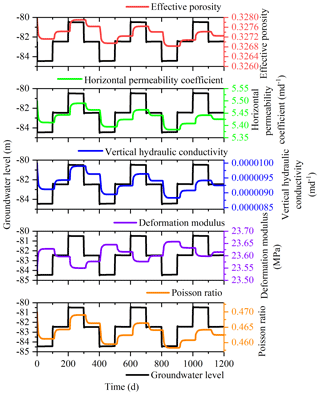
This study was undertaken in order to accurately analyze the land subsidence that is caused by the change in the seepage and stress fields during the pumping and recharge of groundwater. Based on Biot's consolidation theory and groundwater seepage theory (combined with theory regarding the nonlinear rheology of soil), the constitutive relationship of soil was extended to viscoelastic plastic; concurrently, considering the dynamic changes in hydraulic parameters and soil mechanical parameters, a three-dimensional fully coupled model of groundwater seepage and soil deformation was established. Using the groundwater recycling pumping and recharge test conducted by Land Subsidence Monitoring and Early Warning Center in Cangzhou City as an example, the site was divided into four loose porous aquifers. A constantly circulating pumping–recharge flow was simulated numerically, and numerical simulation was carried out on the third and fourth confined aquifers. The influence of groundwater seepage on soil deformation was analyzed, and the variation in hydraulic parameters and soil mechanical parameters were studied under the influence of the abovementioned cyclic pumping and recharge. The results show that soil deformation lags behind the change in the groundwater level, and that permanent residual deformation of soil is produced by water level fluctuations during groundwater pumping–recharge cycles. The effective porosity, the permeability coefficient and the Poisson ratio are positively correlated with the water level fluctuation in groundwater pumping–recharge cycles, whereas the modulus of deformation is negatively correlated with the water level fluctuation in groundwater during this process. All parameters change, and this change is permanent. The simulated results are in good agreement with the measured values.